Переход от эйлерова описания к лагранжевому и обратно
Эйлерово и лагранжево описание являются равносильными и нужно уметь переходить от одного описания к другому. Рассмотрим этот вопрос на примере.
Пример 1. Дано эйлерово описание движения сплошной среды
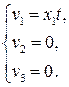
Требуется найти его лагранжево описание.
Решение.
Зададим материальные координаты так, что в начальный момент движения они равны геометрическим, т.е. при 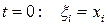 . Учитывая определение скорости и начальное условие, имеем задачу Коши для системы уравнений
. Учитывая определение скорости и начальное условие, имеем задачу Коши для системы уравнений
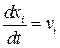 ,
,
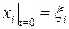 .
.
Решим эту задачу.
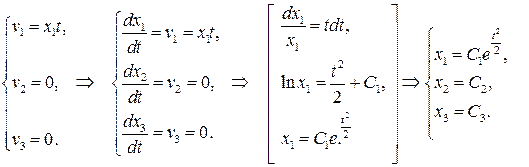
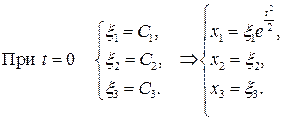
Закон движения в лагранжевых переменных найден.
Таким образом, чтобы перейти от эйлерова описанию к лагранжевому, необходимо составить систему 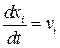 и решить ее с учетом начальных условий
и решить ее с учетом начальных условий 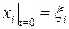 .
.
Убедимся, что 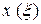 и
и 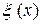 – взаимнооднозначные зависимости, т.е. в любой момент времени в любой точке пространства находится только одна материальная частица. Для этого нужно вычислить якобиан и убедиться, что он никогда не обращается в нуль.
– взаимнооднозначные зависимости, т.е. в любой момент времени в любой точке пространства находится только одна материальная частица. Для этого нужно вычислить якобиан и убедиться, что он никогда не обращается в нуль.
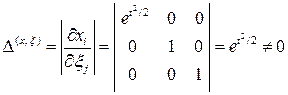
для любого момента времени.
Следовательно, зависимость 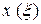 взаимнооднозначная. Известно, что
взаимнооднозначная. Известно, что 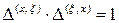 . Отсюда следует, что обратная зависимость также взаимнооднозначная. В этом можно убедиться и непосредственно, вычислив якобиан обратного преобразования
. Отсюда следует, что обратная зависимость также взаимнооднозначная. В этом можно убедиться и непосредственно, вычислив якобиан обратного преобразования
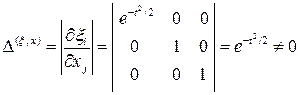
для любого момента времени.
Найдем выражения для скорости и ускорения в лагранжевых переменных. Чтобы выразить скорость, достаточно геометрические координаты заменить на материальные, используя для этого закон движения в лагранжевых переменных. Получим
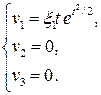
Найдем ускорение, которое вычисляется как материальная производная скорости. Напомним, что при лагранжевом описании материальная производная совпадает с частной производной по времени.
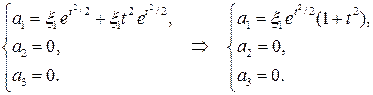
Пример 2. Дано лагранжево описание движения сплошной среды
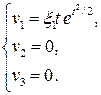
Требуется найти его эйлерово описание.
Решение.
Учитывая определение скорости и начальное условие, имеем задачу Коши для системы уравнений:
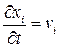 ,
,
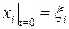 .
.
Подставим в систему заданное выражение для скорости и проинтегрируем по времени. Получим, проделав несложные выкладки, эйлерово описание:
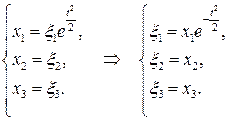
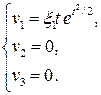
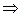
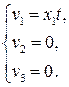
Найдем ускорение, которое вычисляется как материальная производная скорости 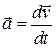 :
:
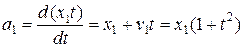 .
.
Можно вычислить иначе:
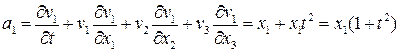 ,
,
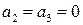 .
.
Третий путь состоит в том, чтобы вычислить ускорение в лагранжевых переменных (см. Пример 1), и потом заменить в его выражении материальные координаты на геометрические, как выше было сделано для скорости.
Окончательно:
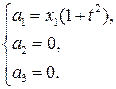
Дата добавления: 2015-12-29; просмотров: 6977;
