Траектории и линии тока

Траекториейматериальной частицы называется линия, которую частица описывает в процессе движения.

Дифференциальное уравнение траектории имеет вид:

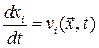или .

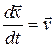Решив его, найдем параметрическое уравнение траектории рассматриваемой частицы с материальной координатой ξ:

.

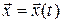Линией тока называется такая линия, касательная к которой в каждой точке совпадает с направлением скорости сплошной среды в этой точке в данный момент времени (Рис.1.3.1).

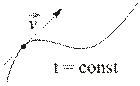Рис.1.3.1

Из определения следует, что линия тока есть векторная линия поля скоростей сплошной среды.

Линия тока рассматривается для фиксированного момента времени, траектория описывает перемещение частицы в пространстве с течением времени.

Получим уравнение линии тока в параметрической форме с параметром .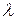

По определению в любой фиксированный момент времени 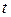вектор касательной к линии тока 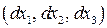коллинеарен вектору скорости 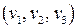. Поэтому

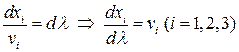
– дифференциальное уравнение линии тока.

Поверхностью (трубкой) тока называется поверхность, состоящая из линий тока, проведенных через каждую точку некоторого контура, не являющегося линией тока.

Если скорость сплошной среды 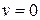или 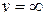в некоторой точке, то эта точка называется особой точкой.

Теорема. Через каждую неособую точку проходит единственная линия тока.

Данная теорема следует из теоремы существования и единственности решения задачи Коши для системы обыкновенных дифференциальных уравнений.

Примеры особых точек.

1. Круг на плоскости обтекается жидкостью, в лобовой точке 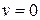и линия тока раздваивается в этой точке.

2. Источник или сток. Из точки равномерно во все стороны вытекает жидкость (источник), в этой точке 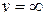, линий тока бесконечно много.

Движение абсолютно твердого тела называется поступательным, если все точки тела перемещаются с одинаковой скоростью .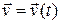

Примеры траекторий и линий тока.

1. Произвольное поступательное движение абсолютно твердого тела.

Траектории – любые линии. Найдем уравнение линий тока.

,

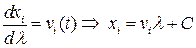то есть линии тока – прямые линии.

2. Прямолинейное поступательное движение абсолютно твердого тела.

Траектории - прямые линии и совпадают с линиями тока. Заметим, что модуль скорости может меняться, но ее направление остается постоянным. Этого оказывается достаточно, чтобы траектории и линии тока совпадали.

3. Вращательное движение абсолютно твердого тела вокруг оси.

Траектории и линии тока являются окружностями с центром на оси и совпадают.

4. Произвольное движение абсолютно твердого тела.

Траектории – любые линии, линии тока – винтовые линии.

1.3.2. Установившиеся и неустановившиеся
движения сплошной среды

Движение называется установившимся (стационарным), если при эйлеровом описании параметры движения не зависят от времени.

Заметим, что в стационарном движении ускорение может быть отлично от нуля. Далее, из определения следует, что движение может быть стационарным или нестационарным в зависимости от выбора системы координат наблюдателя.

Моделирование стационарного движения может оказаться легче, так как параметры будут зависеть от трех аргументов вместо четырех. Но иногда решение стационарной задачи бывает сложнее, чем нестационарной.

Теорема. Если движение стационарное, то линии тока и траектории совпадают.

◄ Для стационарного движения 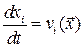и 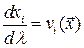. Видно, что отличие лишь в обозначении параметра интегрирования, следовательно, решения этих уравнений, то есть линии тока и траектории, совпадают. ►

Замечание. Пусть движение нестационарное и 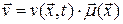, т.е. модуль скорости зависит от времени, а направление нет. Линия тока связана с направлением скорости, следовательно, она со временем меняться не будет и линии тока и траектории совпадут.