Ортогональное преобразование координат
В дальнейшем будем пользоваться правой декартовой прямоугольной системой координат в пространстве. Такую систему можно задать ортонормированным базисом 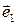 ,
, 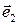 и
и 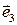 .
.
Преобразование, которое переводит одну правую декартову прямоугольную систему координат 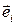 в другую правую декартову прямоугольную систему координат
в другую правую декартову прямоугольную систему координат 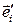 с тем же началом, называется ортогональным.
с тем же началом, называется ортогональным.
Пусть система 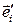 получена из системы
получена из системы 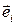 ортогональным преобразованием – поворотом. Каждый вектор базиса
ортогональным преобразованием – поворотом. Каждый вектор базиса 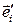 может быть разложен по базису старой системы:
может быть разложен по базису старой системы:
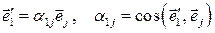 .
.
Аналогично для 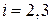 .
.
Таким образом, формулы преобразования имеют вид:
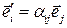 .
.
Формулы обратного преобразования имеют вид:
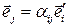 .
.
Составим матрицу ортогонального преобразования:
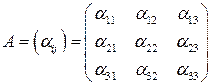 .
.
Видно, что 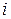 -я строка матрицы составлена из координат вектора
-я строка матрицы составлена из координат вектора 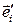 в системе без штрихов,
в системе без штрихов, 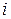 -й столбец – из координат вектора
-й столбец – из координат вектора 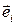 в системе со штрихом.
в системе со штрихом.
Символом Крóнекера называется функция
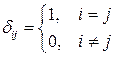
Свойства матрицы ортогонального преобразования:
1. 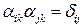
Матрица, обладающая свойством 1, называется ортогональной.
2. 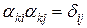
3. Транспонированная матрица 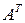 является ортогональной, кроме того
является ортогональной, кроме того 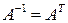 ,
, 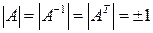 .
.
Любой вектор 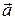 может быть разложен по базису
может быть разложен по базису
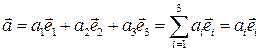 ,
,
где 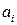 – компоненты вектора
– компоненты вектора 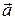 . Получим связь между компонентами вектора в разных системах координат:
. Получим связь между компонентами вектора в разных системах координат:
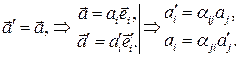
Вектор – это математический объект, который задается тройкой чисел, компонентами 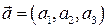 , и при ортогональном преобразовании, заданном матрицей
, и при ортогональном преобразовании, заданном матрицей 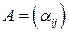 , компоненты вектора преобразуются по следующему правилу:
, компоненты вектора преобразуются по следующему правилу:
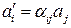 .
.
Это определение равносильно определению вектора как направленного отрезка. Последнее следует из равенства:
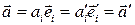 .
.
Можно определить скалярное произведение векторов, модуль вектора и показать, что они инвариантны.
Тензором 2-го ранга T называется математический объект, который задается девятью числами (компонентами) 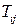 в некоторой системе координат
в некоторой системе координат 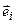 . Причем при преобразовании
. Причем при преобразовании 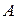 координат
координат 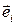 в
в 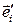 , новые компоненты тензора связаны со старыми следующим соотношением:
, новые компоненты тензора связаны со старыми следующим соотношением:
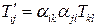
Последнее равенство можно записать в матричной форме:
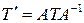 .
.
Можно найти обратное преобразование:
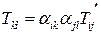 .
.
Тензор является инвариантной величиной, т.е. T´=T, но их компоненты, вообще говоря, не совпадают 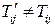 .
.
Тензором n-го ранга T называется математический объект, который задается 3n числами (компонентами) 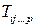 в некоторой системе координат
в некоторой системе координат 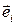 . Причем при ортогональном преобразовании координат
. Причем при ортогональном преобразовании координат 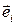 в
в 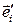 , новые компоненты тензора связаны со старыми следующим соотношением:
, новые компоненты тензора связаны со старыми следующим соотношением:
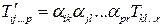 .
.
Дата добавления: 2015-12-29; просмотров: 3178;
