Оператор Гамильтона и его применение к скалярным, векторным и тензорным величинам

Оператором Гамильтона или оператором 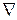(«набла») называется оператор

.

Символ 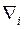обозначает производную по 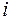-ой координате. Набла ( ) с греческого переводится как арфа.

Пусть 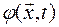– скалярная функция. Результатом применения оператора Гамильтона к скалярной функции являетсявектор

.

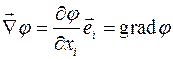Заметим, чтопроизводная по направлению 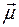скалярного поля 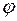равна проекции градиента поля на это направление:

.

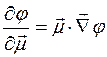Пусть 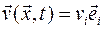– векторная функция. Результатом применения оператора Гамильтона к векторной функции является тензор 2-го ранга

,

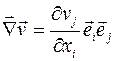который называется векторным градиентом поля .

Покажем, что 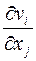– тензор 2-го ранга.

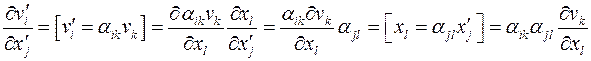Следовательно, по определению 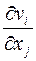– тензор 2-го ранга.

Так же, как для скалярного поля, производная по направлению 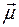векторного поля равна проекции векторного градиента поля на это направление

.

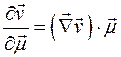Результатом применения оператора Гамильтона к тензору 2-го ранга является тензор 3-го ранга

.

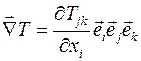Таким образом, применение оператора 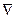повышает ранг тензора на единицу.

С помощью символа (но не оператора!) 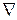можно также записать выражение для дивергенции и вихря (ротора) векторной функции:

,

.

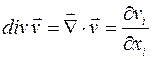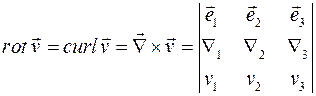Следует обратить внимание, что символом 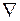не всегда можно пользоваться как вектором. Например, смешанное произведение трех векторов есть скаляр

.

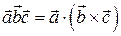С другой стороны, выражение 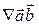есть тензор третьего ранга.

Кроме того, для смешанного произведения векторов справедливо:

.

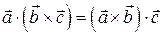Однако, если один из векторов в этом равенстве заменить на оператор 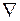, то равенство перестанет быть верным:

.

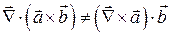Действительно,

,

.

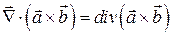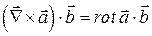Распишем более подробно операции и :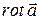

,

.

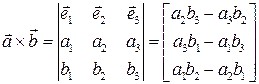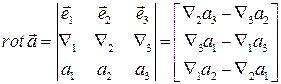Продолжив вычисления, можно убедиться, что .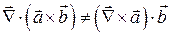

Тензор деформаций