Тензор малых деформаций
Под малыми деформациями понимается движение сплошной среды, при котором длины материальных волокон и углы между ними мало изменяются, то есть относительное удлинение волокон и относительное скашивание первоначально прямых углов между волокнами много меньше единицы. Кроме того, потребуем малость частных производных компонентов перемещений по сравнению с единицей. В этом случае, в выражениях для компонентов тензоров L и E произведением малых величин можно пренебречь. Таким образом, линеаризованные тензоры деформаций или тензоры малых деформацийимеют вид:
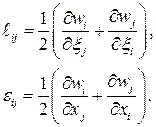
Можно доказать, что тензоры малых деформаций совпадают.
Пример.Пусть движение сплошной среды происходит по закону:
 .
.
Найдем тензор L. Для этого сначала вычислим компоненты вектора перемещений в лагранжевых координатах:
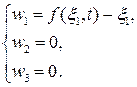 .
.
Из всех компонентов тензора L ненулевым будет только один –  .
.
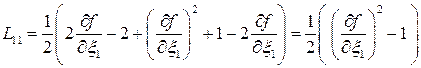 .
.
Найдем тензор E. Сначала вычислим компоненты вектора перемещений в эйлеровых координатах:
 .
.
Тензор E имеет только один ненулевой компонент:
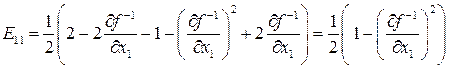 .
.
В нашем случае
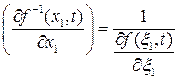 .
.
Поэтому нетрудно найти 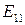 в лагранжевых координатах:
в лагранжевых координатах:
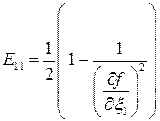
Видно, что 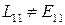 . То есть лагранжев и эйлеров тензор конечных деформаций не совпадают.
. То есть лагранжев и эйлеров тензор конечных деформаций не совпадают.
Найдем лагранжев и эйлеров тензоры малых деформаций и покажем, что они совпадают.
Пусть 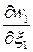 =
=  . Тогда
. Тогда
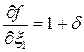 ,
,
 =
= 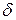 .
.
Вычислим  . Так как в линейном приближении
. Так как в линейном приближении
 ,
,
то
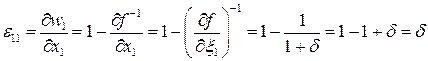
Итак, 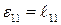 .
.
Перейдем к вычислению относительного изменения длины материального элемента при малых деформациях:
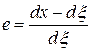 .
.
Отсюда следует, что
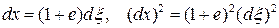 .
.
В силу малости деформаций относительное изменение длины мало, следовательно, в линейном приближении квадратом этой величины можно пренебречь:
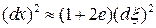 .
.
Далее
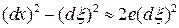 .
.
Отсюда
 .
.
Относительное изменение длины отрезка выразим через лагранжев или эйлеров тензор малых деформаций, получим:
 ,
, 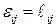 .
.
Можно ввести единичный вектор 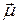 в направлении рассматриваемого отрезка
в направлении рассматриваемого отрезка 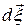 :
:
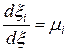 .
.
Тогда формулу для 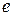 можно переписать в матричном виде:
можно переписать в матричном виде:
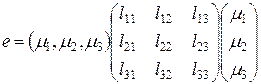 ,
,
или
 .
.
Дата добавления: 2015-12-29; просмотров: 2105;
