Исследование статической устойчивости методом малых колебаний

Если СЭС описывается уравнениями невысокого порядка, то для оценки статической устойчивости режима можно использовать метод малых колебаний. В отличие от оценки статической устойчивости по практическим критериям суть этого метода заключается в исследовании уравнений движения, записанных в виде уравнений малых отклонений.

Пусть состояние СЭС в любой момент времени описывается дифференциальным нелинейным уравнением возмущенного движения вида

(52)

где y_i -совокупность показателей режима СЭС, которые являются функциями времени;

f_i - внешние воздействия, изменение которых может быть произвольным.

В состоянии равновесия СЭС характеризуется установившимися значениями (y_i0)этих показателей:

(53)

Левую часть уравнения (12.53) можно выразить через малые отклонения x_i=y_i-y_i0 показателей режима 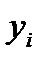от установившихся значений y_i0,записав

(54)

Здесь составляющие, которые содержат x_i характеризуют переходный процесс X(t), вызванный возмущениями.

Начальные условия для переходного процесса при t=t₀.

(55)

В случае невозмущенного движения x_i=0.

Оценка устойчивости на основе систем уравнений вида (54) обоснована теоремами А. М. Ляпунова.

При решении инженерных задач можно руководствоваться физической трактовкой приведенных определений устойчивости в отношении характера переходного процесса 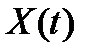no его амплитуде.

При апериодической устойчивости переходный процесс по амплитуде затухающий.

При колебательном процессе сохранение устойчивости будет при неизменной амплитуде колебаний

Нарушение устойчивости будет при увеличении амплитуды колебаний.

Характер переходного процесса можно установить также из анализа системы нелинейных дифференциальных уравнений (54). Она линеаризуется методом первого приближения А. М. Ляпунова, после чего анализируется вид корней характеристического уравнения системы линеаризованных уравнений. В основе линеаризации лежит предположение о таком изменении переменных в переходном процессе, при котором их отклонения от установившихся значений остаются все время достаточно малыми.

Линеаризацию системы уравнений (54) выполняют разложением левой части уравнений в степенной ряд (Тейлора или Маклорена) по степеням малых отклонений x_i(все производные от x_i рассматриваются как самостоятельные переменные).

(56)

После некоторых преобразований получим линеаризованные уравнения возмущенного движения (уравнения первого приближения), приведенных к более компактной записи:

(57)

Об устойчивости нелинейной системы (56) судят по затуханию переходного процесса, наличие которого устанавливается по виду корней характеристического уравнения системы (57):

(58)

Для устойчивости необходимо и достаточно, чтобы корни характеристического уравнения имели отрицательные вещественные части.

Если не все коэффициенты характеристического уравнения имеют одинаковый знак, то невозмущенное движение неустойчиво и дополнительно устойчивость можно не исследовать.

Применяемые критерии устойчивости делятся на алгебраические (Гурвица, Льенара - Шипара, Рауса) и частотные (Михайлова, Найквиста, логарифмический). Используется также метод D-разбиения.

Критерий Гурвица определяет условия устойчивости системы по характеристическому уравнению (58). Для этого составляют определитель из n строк и nстолбцов:

(59)

Критерий Льенара — Шипара для устойчивости системы требует выполнения двух условий:

1) коэффициенты характеристического уравнения (58) должны быть положительными, т. е. a_s>0, (s=0,1,2,…,n);

2) диагональные миноры (n-1) и (n-3) определителя (59) должны быть положительными, т. е.

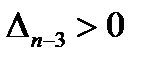(60)

Критерий Рауса для устойчивости системы также требует выполнения двух условий:

1) коэффициенты характеристического уравнения (58) должны быть положительными;

2) коэффициенты первого столбца таблицы Рауса (табл.2), содержащей n+1 строку, должны быть положительными.

Таблица2. Таблица Рауса

Номера i-й строки	Номера к-го столбца	Коэффициенты
				…
…	…	…	…	…	… … … … …	- - …

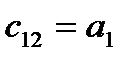
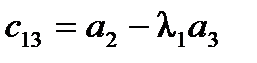
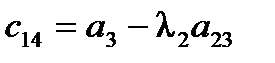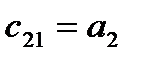
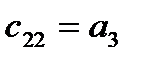
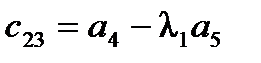
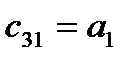
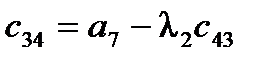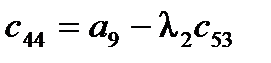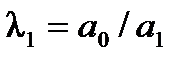
Критерий Михайлова при анализе условий устойчивости системы позволяет получить их наглядную геометрическую интерпретацию.

Рис. 26. Кривые Михайлова для устойчивых систем уравнений n-го порядка (а) и траектория кривой Михайлова для границ устойчивости первого (1), второго (2) и третьего (5) типов (б)

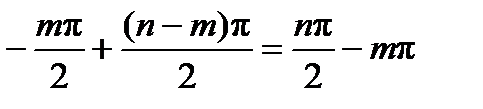(61)

Выражение (61) иллюстрирует сформулированный А. В. Михайловым критерий устойчивости для линейной системы уравнений n-го порядка:

если характеристический радиус-вектор в точке кривой Михайлова при последовательном изменении угловой скорости в пределах от 0 до +∞ имеет результирующий угол поворота +nπ/2, то решение системы уравнений устойчиво.