Практические критерии оценки статической устойчивости
Анализ статической устойчивости по его возрастающей сложности можно разбить на несколько этапов:
следует установить факт наличия устойчивости или неустойчивости установившегося режима;
по виду кривой или другим признакам различить характер переходного процесса (апериодический или колебательный).
Физически апериодическая неустойчивость возникает при нарушении баланса моментов на валу генератора, когда механический момент турбины превышает максимально возможный при данных условиях электромагнитный момент генератора.
Анализ устойчивости заключается в определении предельных по устойчивости режимов на основе сползания или текучести параметров нормального режима с использованием уравнений установившегося режима.
Для установленной области устойчивых режимов выявляются условия колебательной неустойчивости, которая может появиться по следующим причинам:
из-за наличия параметрического самораскачивания или обратной связи в виде АРВ;
при возникновении самовозбуждения, когда синхронный генератор нагружен емкостью или линией с распределенными параметрами;
из-за неустойчивости нагрузки.
Анализ колебательной устойчивости предполагает учет динамики элементов системы посредством ее модели, описываемой дифференциальными уравнениями. При этом ставится и решается задача определения структуры и параметров элементов регулирующих устройств для обеспечения статической устойчивости режимов системы.
Наличие устойчивости или неустойчивости установившегося режима при относительно малых текущих изменениях его параметров («сползании» показателей установившегося режима) можно определить с помощью практических критериев, основанных на физических представлениях о механизме нарушения устойчивости. Они применяются в тех случаях, когда отсутствуют условия самораскачивания и нет необходимости в исследованиях характера переходного процесса и в выявлении формы нарушения устойчивости (апериодическая или колебательная). Оценка устойчивости по практическим критериям является грубой, завышенной по запасу устойчивости и устанавливает лишь сам факт устойчивости данного режима.
Физическая оценка механизма нарушения устойчивости выполняется на основе энергетического или силового подхода.
При энергетическом подходе условия устойчивости определяются согласно теореме Дирихле:
система будет устойчивой, если потенциальная энергия консервативной системы в положении равновесия имеет минимум.
При силовом подходе устойчивость системы определяется условием, согласно которому в положении равновесия сумма приложенных к телу сил должна быть равной нулю.
Оценка статической устойчивости по практическим критериям позволяет установить предельный режим и границу устойчивости при выбранном способе воздействия на СЭС. Последний называют способом утяжеления режима. Он может быть выбран только при условии, если заданы схема электроснабжения и состав электроприемников.
Расчетные схемы электроснабжения могут приводиться к различным видам:
эквивалентный генератор - ЛЭП - шины неизменного напряжения;
двустороннее питание нагрузки с постоянным сопротивлением;
эквивалентный источник питания - узловая точка сети;
питание асинхронной нагрузки от мощной ЭЭС;
эквивалентный источник, питающий комплексную нагрузку соизмеримой мощности.
Рассмотрим некоторые примеры использования практических критериев для анализа статической устойчивости этих схем.
Схема электроснабжения «эквивалентный генератор - ЛЭП - шины неизменного напряжения».
Эта схема с параметрами ее элементов показана на рис.23. В установившемся режиме механический момент турбины и электромагнитный момент генератора уравновешены, т. е.
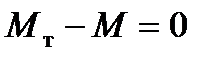 (45)
(45)
где электромагнитный момент
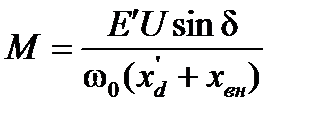 (46)
(46)
имеет только одну существенную переменную δ, так как другие параметры (Е', U, ω0) по условию неизменны. Механический момент турбины находится по формуле
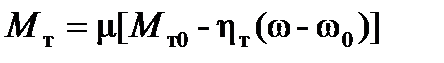 (47)
(47)
Из (47) следует, что Мт не зависит от переменной δ.
Выражая параметры системы в относительных единицах и считая ее частоту неизменной, можно принять 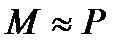 и представить уравнение (45) в следующем виде:
и представить уравнение (45) в следующем виде:
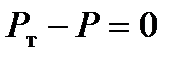 (48)
(48)
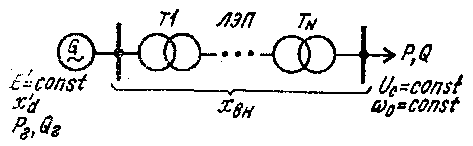
Рис.23. Схема электроснабжения «эквивалентный генератор — ЛЭП — шины неизменного напряжения»
Графическое изображение (48) в зависимости от переменной δ (см. рис.9) показывает, что существуют две точки равновесия режима системы. Нарушение равенства мощностей (48) является признаком изменения ее энергетического баланса и появления избыточной энергии в системе. В этом случае энергетический критерий (12) можно записать так:
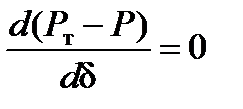 (49)
(49)
Поскольку Рт(δ)=const, неравенство (49) принимает вид 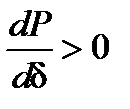 .
.
Схема с двусторонним питанием нагрузки. Для этой схемы, имеющей постоянное сопротивление нагрузки (рис.1.1), энергетический критерий (12) можно косвенно характеризовать переменной режима - активной мощностью.
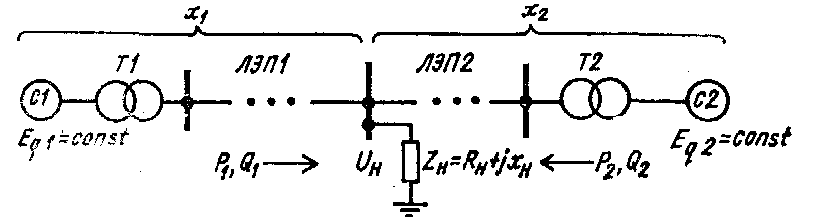
Рис.1.1. Схема двустороннего питания нагрузки (za = const)
Если допустить, что генераторные ветви имеют одинаковую нагрузку 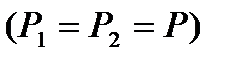 ,то установившийся режим будет описываться следующей системой уравнений;
,то установившийся режим будет описываться следующей системой уравнений;
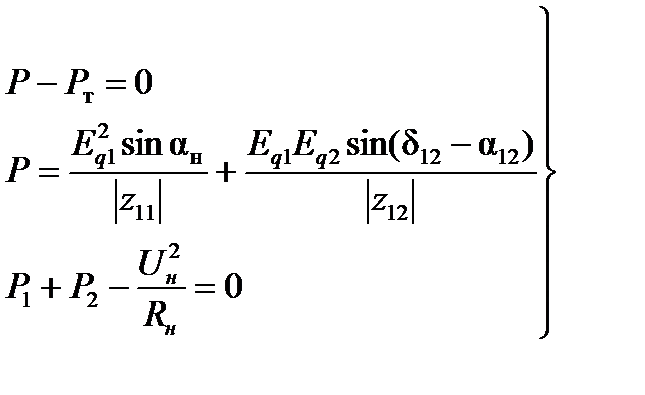 (1.1)
(1.1)
где
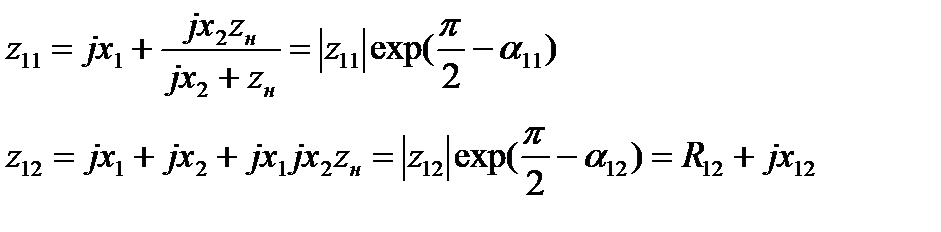
В уравнениях (1.1) свободной существенной переменной, от которой зависят изменяющиеся параметры режима 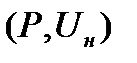 , является угол δ12. Поэтому производную
, является угол δ12. Поэтому производную 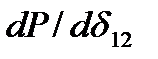 можно использовать в качестве практического критерия статической устойчивости аналогично выражению (17):
можно использовать в качестве практического критерия статической устойчивости аналогично выражению (17):
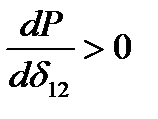 (1.2)
(1.2)
Предельный по сохранению устойчивости режим соответствует условию
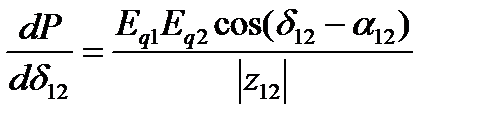 (1.3)
(1.3)
откуда
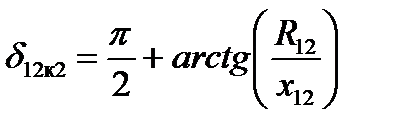 (1.4)
(1.4)
Подставив (1.4) в уравнение активной мощности генераторной станции (1.1), получим критическое значение переменной режима для угловой характеристики мощности:
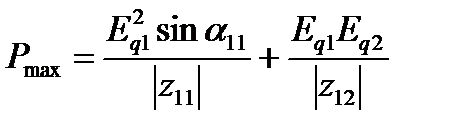 (1.5)
(1.5)
Коэффициент запаса статической устойчивости определяется выражением
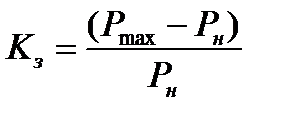 (1.6)
(1.6)
Схема замещения электрической системы, содержащая узловую точку.Анализ этой схемы (рис. 1.2) упрощается. Объясняется это тем, что нагрузки, подключенные к узловым точкам сложных СЭС, могут замещать части системы и задаваться статическими (43) или динамическими (44) характеристиками. Узлы характеризуются векторами напряжения, которые играют роль эквивалентных э. д. с. неявных источников и нагрузок и отличаются от явных тем, что они не обладают инерционностью генераторов и нагрузок двигателей.
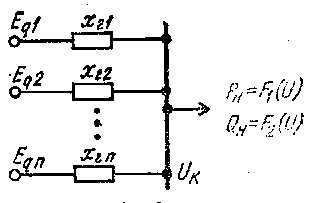
Рис.1.2. Схема замещения электрической системы с узловой точкой
Практический критерий статической устойчивости режима рассматриваемой системы можно сформулировать при неизменной частоте, сохранении баланса активной мощности в узле и постоянстве активной мощности, передаваемой из генераторных ветвей 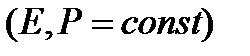 . Из анализа множества изменяющихся параметров режима
. Из анализа множества изменяющихся параметров режима 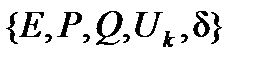 следует, что существенной независимой переменной, определяющей состояние всех элементов системы, является напряжение в узловой точке
следует, что существенной независимой переменной, определяющей состояние всех элементов системы, является напряжение в узловой точке 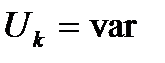 (переменная δ в данном случае не существенна, так как она не определяет состояние нагрузки).
(переменная δ в данном случае не существенна, так как она не определяет состояние нагрузки).
Избыточная энергия системы, возникающая из-за возмущающих воздействий, проявляется как изменение баланса реактивной мощности (42) узла:
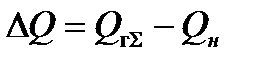 (1.7)
(1.7)
где 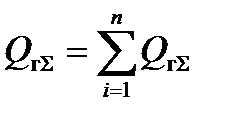 - суммарная генерируемая реактивная мощность в узле.
- суммарная генерируемая реактивная мощность в узле.
Взаимосвязь этих существенных переменных в установившемся режиме определяется уравнением
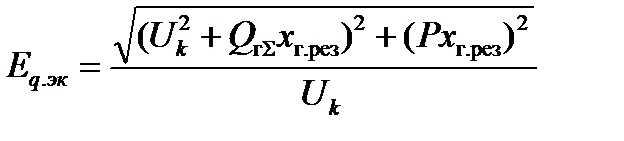 (1.8)
(1.8)
где
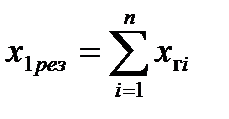 ;
; 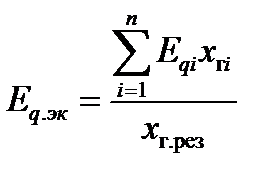 ;
; 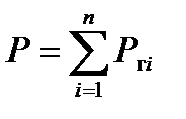
Практический критерий устойчивости такой системы в соответствии с (12) можно записать в виде
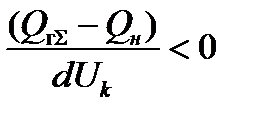 (1.9)
(1.9)
Он характеризует реакцию системы на изменение напряжения в узле. Появление небаланса реактивной мощности в узле рассматривается как малое возмущение, под воздействием которого изменяется напряжение.
Исследование системы по этому критерию заключается в анализе по переменной 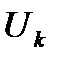 уравнений установившегося режима:
уравнений установившегося режима:
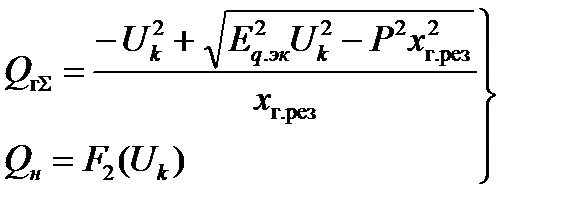 (1.10)
(1.10)
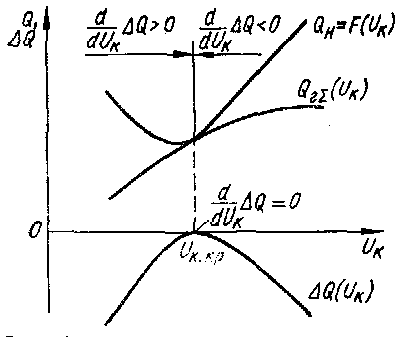
Рис. 1.3. Графическое решение системы уравнений (1.10) и (1.7)
Здесь уравнение генерируемой реактивной мощности получено преобразованием уравнения (1.8).
Систему уравнений (1.10) решают аналитически или графически в зависимости от способа задания статической характеристики нагрузки (43). Решение соответствует следующим критическим значениям существенных параметров режима: 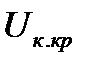 и
и 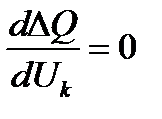 (рис. 1.3). Знак производной (1.9) проверяют, начиная с заведомо устойчивого состояния, с постепенным пошаговым его утяжелением по показателю
(рис. 1.3). Знак производной (1.9) проверяют, начиная с заведомо устойчивого состояния, с постепенным пошаговым его утяжелением по показателю 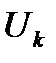 . На основе результатов вычислений по уравнениям (1.7) и (1.10) строят кривую небаланса реактивной мощности
. На основе результатов вычислений по уравнениям (1.7) и (1.10) строят кривую небаланса реактивной мощности 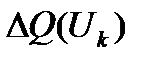 , на которой выявляют экстремальную точку критического напряжения.
, на которой выявляют экстремальную точку критического напряжения.
Коэффициент запаса статической устойчивости определяют через показатели установившегося и предельного режимов:
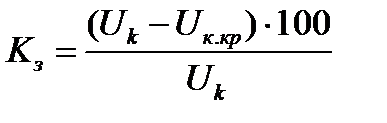 (1.11)
(1.11)
Питание асинхронной нагрузки от мощной ЭЭС.В этом случае предполагается, что последняя обладает бесконечной мощностью, имеет узловую точку неизменного напряжения или точку, питающуюся от эквивалентного источника с неизменной э. д. с. Ее схема замещения показана на рис. 1.4,а,где нагрузка представлена в виде эквивалентного асинхронного двигателя согласно рис. 22.
Выполним анализ статической устойчивости асинхронной нагрузки для данного случая при переменной и постоянной потребляемой активной мощности.
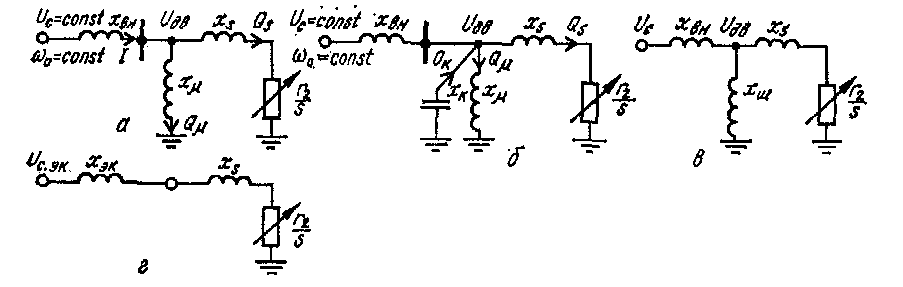
Рис. 1.4. Схемы замещения СЭС с асинхронной нагрузкой (а - без компенсации реактивной мощности; б - с компенсацией) и их упрощения (в, г)
При изменении активной мощности, потребляемой нагрузкой, состояние равновесия установившегося режима для данной схемы описывается уравнениями
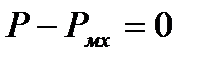 (1.12)
(1.12)
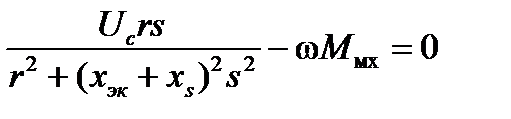 (1.13)
(1.13)
где первое слагаемое - потребляемая асинхронным двигателем активная мощность, а второе слагаемое определяется моментом сопротивления рабочего механизма.
Уравнение (1.13) содержит только одну существенную переменную - скольжение s, а другие параметры и показатели в установившемся режиме постоянны. Действие возмущений влияет только на баланс активной мощности в точке включения нагрузки, нарушение которого можно оценить по критерию
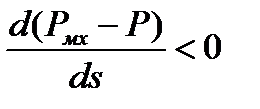 (1.14)
(1.14)
откуда при 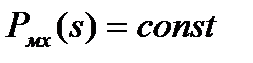 получаем
получаем
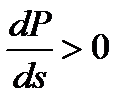 (1.15)
(1.15)
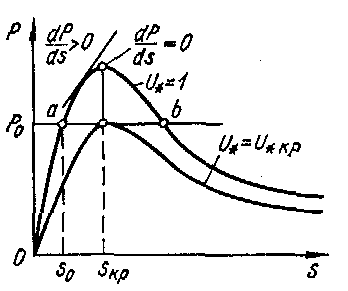
Рис. 1.512.8. Характеристики эквивалентного асинхронного двигателя
При положительном значении критерия (1.15) работа асинхронной нагрузки устойчива. Предел сохранения устойчивости имеет место при 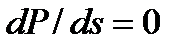 (рис.1.5). Физически производная
(рис.1.5). Физически производная 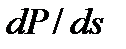 характеризует реакцию СЭС на увеличение скольжения s асинхронной нагрузки. При положительном знаке производной случайному повышению скольжения соответствует электромагнитная мощность, которая отбирается из электрической сети и которая возрастает быстрее, чем тормозящая статическая мощность рабочего механизма. Избыток мощности при этом приводит к ускорению двигателей, в результате чего рабочая точка режима возвращается к скольжению, которое соответствует исходному состоянию.
характеризует реакцию СЭС на увеличение скольжения s асинхронной нагрузки. При положительном знаке производной случайному повышению скольжения соответствует электромагнитная мощность, которая отбирается из электрической сети и которая возрастает быстрее, чем тормозящая статическая мощность рабочего механизма. Избыток мощности при этом приводит к ускорению двигателей, в результате чего рабочая точка режима возвращается к скольжению, которое соответствует исходному состоянию.
Из уравнения установившегося равновесия (1.13) и утяжеления режима по переменной s можно определить по критерию (1.15) критические значения изменяющихся параметров 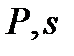 для предельного по устойчивости состояния (см. рис. 1.5). При
для предельного по устойчивости состояния (см. рис. 1.5). При 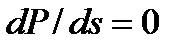 имеем
имеем
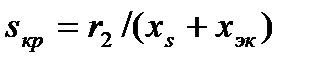 (1.16)
(1.16)
Подставив 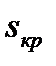 в уравнение (40), получим наибольшее значение активной мощности, потребляемой нагрузкой,
в уравнение (40), получим наибольшее значение активной мощности, потребляемой нагрузкой,
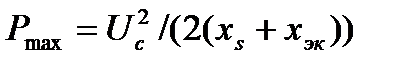 (1.17)
(1.17)
которое соответствует опрокидывающему моменту эквивалентного асинхронного двигателя.
Поскольку опрокидывающий момент пропорционален квадрату напряжения на зажимах двигателя, со снижением напряжения он уменьшается. Напряжение, при котором опрокидывающий момент становится равным нагрузке двигателя, называется критическим (см. рис. 1.5). Определяется оно выражением
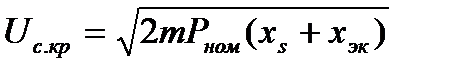 (1.18)
(1.18)
где 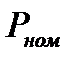 - номинальная мощность эквивалентного двигателя;
- номинальная мощность эквивалентного двигателя; 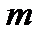 - коэффициент его загрузки.
- коэффициент его загрузки.
При напряжении, меньшем чем критическое,, двигатели узла нагрузки затормаживаются. Значение критического напряжения совместно с 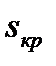 и
и 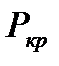 для предельного режима характеризует слепень устойчивости асинхронной нагрузки, причем чем выше критическое напряжение, тем ниже устойчивость двигателей.
для предельного режима характеризует слепень устойчивости асинхронной нагрузки, причем чем выше критическое напряжение, тем ниже устойчивость двигателей.
Согласно (1.18) запас устойчивости зависит от загрузки двигателей 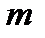 , их электрической удаленности
, их электрической удаленности 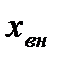 от шин неизменного напряжения и компенсации реактивной мощности в точке включения нагрузки. Эквивалентное сопротивление
от шин неизменного напряжения и компенсации реактивной мощности в точке включения нагрузки. Эквивалентное сопротивление 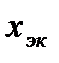 определяется условиями связи рассматриваемой точки системы с шинами неизменного напряжения;
определяется условиями связи рассматриваемой точки системы с шинами неизменного напряжения; 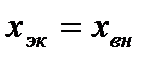 при
при 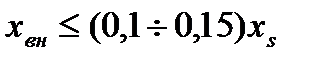 .
.
В случае больших внешних сопротивлений необходимо перейти к эквивалентной схеме замещения, показанной на рис. 1.4 г, где
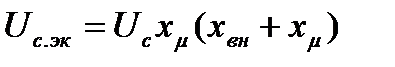 ;
; 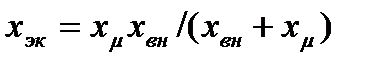 (1.19)
(1.19)
При включении в узле нагрузки статических компенсирующих конденсаторов мощностью 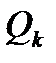 и сопротивлением
и сопротивлением 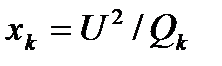 вначале определяют сопротивление эквивалентного шунтапо формуле
вначале определяют сопротивление эквивалентного шунтапо формуле
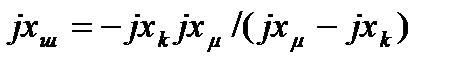
а затем осуществляют переход к схеме замещения по (1.19) при условии 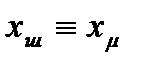 .
.
Напряжение в точке включения нагрузки не является независимой переменной, так как оно определяется режимом работы; узла нагрузки:
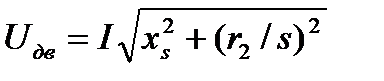
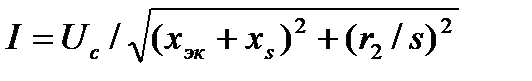
откуда
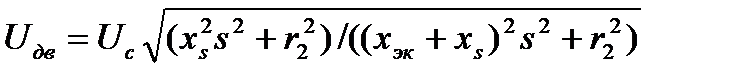 (1.20)
(1.20)
В данном случае критические значения показателей предельного режима нельзя рассчитывать с учетом напряжения, определяемого по (11.20). Они могут быть найдены только по напряжению в системе 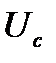 , которое по условию от изменений режима не зависит.
, которое по условию от изменений режима не зависит.
При постоянной потребляемой активности мощности 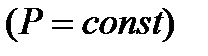 избыточная энергия электрической системы может быть оценена; по балансу реактивной мощности:
избыточная энергия электрической системы может быть оценена; по балансу реактивной мощности:
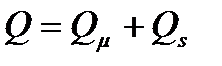 (1.21)
(1.21)
Составляющие (1.21) описываются уравнениями (40), где независимой переменной режима является напряжение в системе
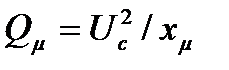 при
при 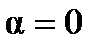 ; (1.22)
; (1.22)
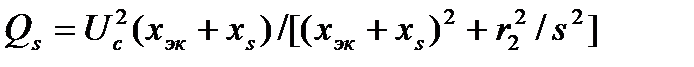 (1.23)
(1.23)
Критические параметры системы определяются на основе анализа (1.24), который выполняют в такой последовательности:
задаются скольжениями s и находят значения тока, соответствующие неизменной нагрузке 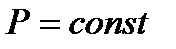 , по формуле
, по формуле
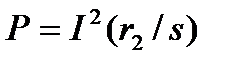
по полученным значениям тока вычисляют ряд напряжений
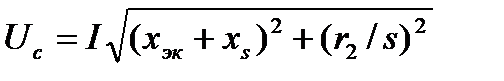
по найденным значениям напряжения определяют составляющие (1.24),
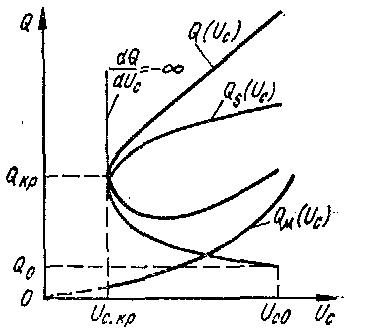
Рис. 1.6. Зависимость реактивной мощности от независимо изменяющегося напряжения в системе
Графический анализ зависимости 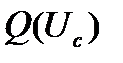 по составляющим
по составляющим 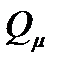 и
и 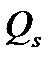 (рис. 1.6) показывает, что предельный режим с критическими значениями параметров
(рис. 1.6) показывает, что предельный режим с критическими значениями параметров 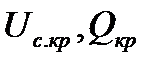 соответствует критерию
соответствует критерию 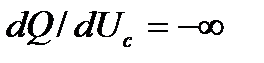 .
.
Дата добавления: 2015-12-08; просмотров: 5589;
