Теорема Коши-Гельмгольца
 Рис. 1.6.1
Рис. 1.6.1
| Рассмотрим материальный объем (Рис.1.6.1). Возьмем в этом объеме произвольную точку 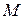 . Если бы объем был твердым телом, то к нему была бы применима теорема о произвольном движении твердого тела: . Если бы объем был твердым телом, то к нему была бы применима теорема о произвольном движении твердого тела:
|
всякое движение тела можно разложить на поступательное со скоростью 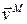 точки
точки 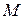 и вращательное с угловой скоростью
и вращательное с угловой скоростью 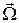 вокруг мгновенной оси, проходящей через эту точку
вокруг мгновенной оси, проходящей через эту точку 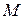 :
:
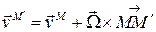 .
.
При этом угловая скорость не зависит от положения точки 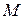 , к которой отнесено вращение твердого тела. Поэтому можно говорить об угловой скорости вращения твердого тела, не указывая эту точку.
, к которой отнесено вращение твердого тела. Поэтому можно говорить об угловой скорости вращения твердого тела, не указывая эту точку.
Для произвольного движения объема сплошной среды справедливо следующее утверждение.
Теорема. Скорость любой точки малого объема сплошной среды в линейном приближении относительно его размера можно представить как сумму скорости поступательного движения, скорости вращательного движения и скорости деформационного движения:
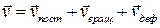 ,
,
причем поступательное и деформационное движения являются потенциальными.
◄ Выделим в материальном объеме произвольную точку 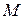 . Пусть
. Пусть 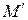 – любая другая точка этого объема,
– любая другая точка этого объема,
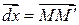 .
.
Разложим скорость частицы 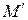 в ряд Тейлора в линейном приближении в окрестности точки
в ряд Тейлора в линейном приближении в окрестности точки 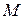 :
:
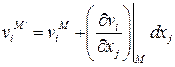 ,
, 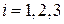 .
.
Представим компоненты 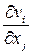 векторного градиента скорости в следующем виде:
векторного градиента скорости в следующем виде:
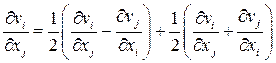 .
.
Введем обозначения:
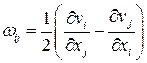 ,
, 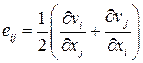 .
.
Тогда
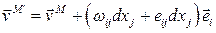 .
.
Тензор 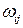 антисимметричный, следовательно, определяется тремя компонентами. Тензор
антисимметричный, следовательно, определяется тремя компонентами. Тензор  есть тензор скоростей деформаций.
есть тензор скоростей деформаций.
Рассмотрим вектор 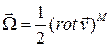 . Можно убедиться непосредственным вычислением, что
. Можно убедиться непосредственным вычислением, что 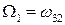 ,
, 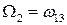 ,
, 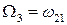 и
и 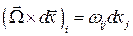 . Но
. Но 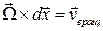 , следовательно
, следовательно 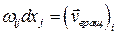 .
.
Назовем вектор с компонентами 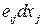 деформационной скоростью
деформационной скоростью 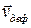 .
.
Таким образом, получим:
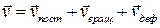 .
.
Покажем, что поступательное и деформационное движения являются потенциальными. Действительно, нетрудно записать потенциал поступательного движения: 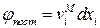
и потенциал деформационного движения: 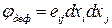 . ►
. ►
Дата добавления: 2015-12-29; просмотров: 5298;
