Закон сохранения массы

В ньютоновской механике любой материальный объем сохраняет свою массу во времени.

Получим закон сохранения массы в дифференциальной форме. Пусть 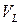– произвольный материальный объем с переменной плотностью (Рис. 1.7.2).

Рис. 1.7.2

Масса, заключенная в этом объеме .

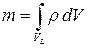Согласно закону сохранения массы

.

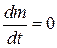Применим следствие 2 из теоремы 3, т.е. формулу

.

Таким образом,

.

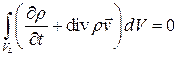Так как объем 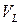выбран произвольно, то по теореме 1

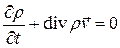
Это дифференциальное уравнение, выражающее закон сохранения массы, называется уравнением неразрывности.

Полученная форма его записи называется дивергентной. Такая форма уравнений в частных производных повышает эффективность процедуры решения с помощью численных методов.

Преобразуем выражение для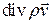

.

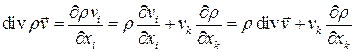Тогда

,

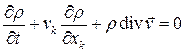Перепишем это равенство иначе

.

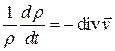Такая формула уравнения неразрывности делает прозрачным его физический смысл: скорость относительного изменения плотности материальной частицы равна скорости относительного изменения ее объема, взятой с противоположным знаком.

Уравнение баланса массы можно записать и для пространственного объема 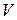, ограниченного поверхностью .

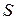В силу следствия 3 из теоремы 3 (формула )

,

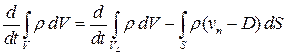где 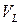– материальный объем, который в момент времени 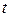совпадает с объемом 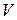. Так как первый интеграл справа равен нулю, то баланс массы для контрольного объема 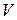имеет вид

.

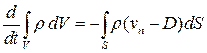Если контрольный объем неподвижен, то 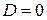. Из интегрального уравнения можно снова получить дифференциальное уравнение неразрывности, рассуждая так же, как в случае материального объема .

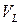Уравнение неразрывности, которое было получено, справедливо при эйлеровом описании движения сплошной среды. При лагранжевом описании оно будет выглядеть иначе.