Массовые и поверхностные силы. Вектор напряжений
В механике сплошной среды различают два типа внешних сил, действующих на элемент объема сплошной среды, – массовые и поверхностные силы.
Массовой силой называется сила, действие которой не зависит от присутствия других частей сплошной среды, кроме рассматриваемого элемента, а численное значение пропорционально массе этого элемента.
Примером массовой силы могут служить сила тяжести (гравитационные силы), электромагнитные силы, силы инерции.
Напряженностью или массовой плотностью поля массовой силы 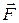 называется массовая сила, отнесенная к единице массы сплошной среды.
называется массовая сила, отнесенная к единице массы сплошной среды.
Например, напряженность силы тяжести равна ускорению свободного падения 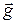 . Для тела, движущегося в инерциальной системе отсчета с ускорением
. Для тела, движущегося в инерциальной системе отсчета с ускорением 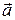 , напряженность даламберовой силы инерции равна
, напряженность даламберовой силы инерции равна 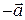 .
.
Поверхностными силами называются силы, приложенные к элементу сплошной среды со стороны прилегающих к нему частиц остальной части сплошной среды. Эти силы действуют на поверхность рассматриваемого элемента. Поверхностная сила, отнесенная к единице площади поверхности, на которую она действует, называется напряжением.
Обозначим через 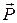 главный вектор поверхностных сил, действующих на площадку
главный вектор поверхностных сил, действующих на площадку 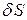 с нормалью
с нормалью 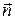 .
.
Напряжение – это удельная поверхностная сила 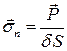 (Рис. 2.1.1).
(Рис. 2.1.1).
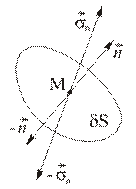 Рис. 2.1.1
Рис. 2.1.1
| Вектор напряжений зависит от ориентации площадки
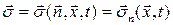 .
Индекс .
Индекс 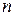 показывает, что напряжение вычислено на площадке с нормалью показывает, что напряжение вычислено на площадке с нормалью 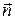 (это не проекция на (это не проекция на 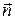 ). ).
|
Обратим внимание, что 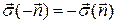 , т.е.
, т.е. 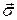 – нечетная функция. Размерность
– нечетная функция. Размерность 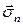 :
: 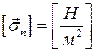 .
.
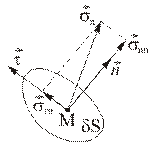 Рис. 2.1.2
Рис. 2.1.2
| Вектор напряжений на площадке с нормалью 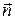 в каждой точке сплошной среды можно разложить на две составляющие – в направлении нормали в каждой точке сплошной среды можно разложить на две составляющие – в направлении нормали 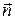 ( ( 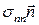 – нормальное напряжение) и касательной – нормальное напряжение) и касательной 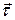 ( ( 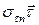 – касательное или сдвиговое напряжение) к площадке – касательное или сдвиговое напряжение) к площадке 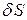 (Рис.2.1.2). (Рис.2.1.2).
|
Совокупность всевозможных векторов напряжений 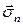 в точке
в точке  определяет напряженное состояние в этой точке. Задача состоит в том, чтобы научиться определять напряжение на площадке с нормалью
определяет напряженное состояние в этой точке. Задача состоит в том, чтобы научиться определять напряжение на площадке с нормалью 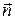 .
.
Тензор напряжений
Пусть задана площадка с нормалью 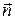 . Нужно научиться определять напряжение на этой площадке.
. Нужно научиться определять напряжение на этой площадке.
Оказывается, что задать напряженное состояние сплошной среды в точке  или, что то же самое, определить правило вычисления вектора напряжений на любой площадке, содержащей эту точку
или, что то же самое, определить правило вычисления вектора напряжений на любой площадке, содержащей эту точку  , можно, задавая векторы напряжений на трех взаимно перпендикулярных площадках в точке
, можно, задавая векторы напряжений на трех взаимно перпендикулярных площадках в точке  .
.
Убедимся в этом. Возьмем точку  за начало системы координат и обозначим через
за начало системы координат и обозначим через 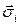 – вектор напряжений на площадке с нормалью
– вектор напряжений на площадке с нормалью 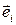 , лежащей на соответствующей координатной плоскости. Разложим векторы напряжений
, лежащей на соответствующей координатной плоскости. Разложим векторы напряжений 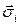 по базису
по базису 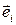 :
:
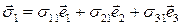 ,
,
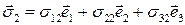 ,
,
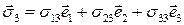 .
.
Девять компонент 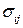 определяют тензор 2-го ранга (докажем это позже), который называется тензор напряжений:
определяют тензор 2-го ранга (докажем это позже), который называется тензор напряжений:
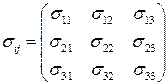 .
.
Заметим, что 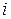 -й столбец матрицы тензора напряжений составлен из компонент вектора напряжений
-й столбец матрицы тензора напряжений составлен из компонент вектора напряжений 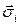 . Разложение тензора напряжений по соответствующему базису имеет вид
. Разложение тензора напряжений по соответствующему базису имеет вид
σ 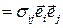 .
.
Рассмотрим механический смысл компонент тензора напряжений. Поясним его на примере компонент 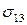 ,
, 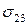 ,
, 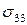 .
.
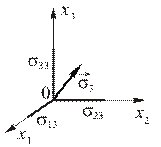 Рис. 2.2.1
Рис. 2.2.1
| Эти компоненты являются компонентами вектора напряжений 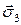 на площадке с нормалью на площадке с нормалью 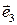 (Рис. 2.2.1). Проекция (Рис. 2.2.1). Проекция
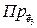 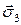 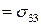
|
дает нормальное напряжение на этой площадке, а проекции
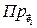
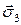
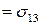 и
и 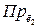
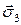
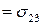
определяют касательные (сдвиговые) напряжения в направлении 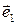 и
и 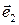 соответственно. Нормальные напряжения связаны с деформаций растяжения, а касательные – с деформацией сдвига. Аналогично можно выяснить механический смысл остальных компонент тензора напряжений.
соответственно. Нормальные напряжения связаны с деформаций растяжения, а касательные – с деформацией сдвига. Аналогично можно выяснить механический смысл остальных компонент тензора напряжений.
Таким образом, диагональные компоненты тензора напряжений задают нормальные напряжения на соответствующих координатных площадках, а недиагональные – сдвиговые напряжения в направлении соответствующих осей координат: 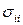 – нормальное напряжение на
– нормальное напряжение на 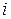 -й координатной площадке,
-й координатной площадке, 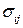 – касательное напряжение.
– касательное напряжение.
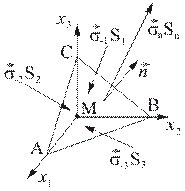 Рис. 2.2.2
Рис. 2.2.2
| Теперь найдем вектор напряжений 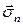 на произвольной площадке с нормалью на произвольной площадке с нормалью 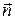 , содержащей точку , содержащей точку  . .
|
Для этого рассмотрим материальный тетраэдр 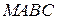 с вершиной в точке
с вершиной в точке  , основанием
, основанием 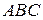 , перпендикулярным нормали
, перпендикулярным нормали 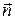 , и боковыми гранями, лежащими на координатных плоскостях (Рис. 2.2.2). Запишем условие равновесия тела
, и боковыми гранями, лежащими на координатных плоскостях (Рис. 2.2.2). Запишем условие равновесия тела 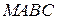 – равенство нулю суммы действующих массовых и поверхностных сил
– равенство нулю суммы действующих массовых и поверхностных сил
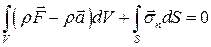 ,
,
где 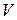 ,
, 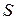 ,
, 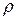 – объем, поверхность и плотность тела соответственно. Массовые силы складываются из внешних сил с напряженностью
– объем, поверхность и плотность тела соответственно. Массовые силы складываются из внешних сил с напряженностью 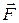 и даламберовых сил инерции с напряженностью
и даламберовых сил инерции с напряженностью 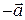 . Поверхностные силы задаются вектором напряжений
. Поверхностные силы задаются вектором напряжений 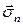 , где
, где 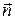 – внешняя нормаль к поверхности
– внешняя нормаль к поверхности 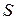 .
.
Обозначим площади основания и боковых граней
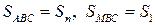 ,
, 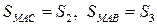 ,
,
причем индексы 1, 2, 3 совпадают с номером координатной оси, перпендикулярной данной грани.
Заметим, что
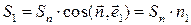 ,
,
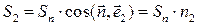 ,
,
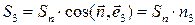 ,
,
так как каждая боковая грань является проекцией основания на соответствующую координатную плоскость.
Таким образом, 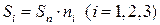 . Объем тетраэдра
. Объем тетраэдра 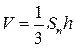 , где
, где 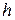 – высота тетраэдра.
– высота тетраэдра.
Интеграл по поверхности 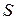 представим как сумму интегралов по граням тетраэдра
представим как сумму интегралов по граням тетраэдра  .
.
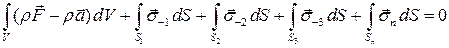 ,
,
где
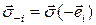 ,
,
причем
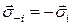 .
.
Применив теорему о среднем к каждому интегралу, получим
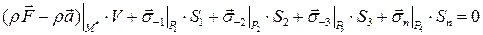
Выразим объем V и площади 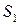 ,
, 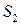 и
и 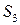 через
через 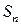 и учтем нечетность функции
и учтем нечетность функции 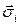 . Получим
. Получим
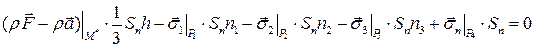 .
.
Так как 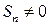 , то поделим на него данное выражение. Устремим
, то поделим на него данное выражение. Устремим 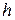 к нулю, при этом грань
к нулю, при этом грань  в пределе совпадет с рассматриваемой площадкой, т.е. в пределе
в пределе совпадет с рассматриваемой площадкой, т.е. в пределе 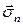 будет искомым напряжением. Точки
будет искомым напряжением. Точки 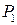 ,
, 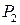 ,
, 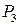 и
и 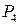 переходят в точку
переходят в точку  . Получим
. Получим
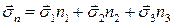
или
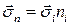 .
.
Выражая через компоненты 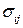 , получим
, получим
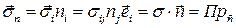 σ,
σ,
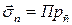 σ.
σ.
Итак, чтобы вычислить вектор напряжений на произвольной площадке с нормалью 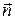 , содержащей точку
, содержащей точку  , нужно найти проекцию тензора напряжений σ, вычисленного в точке
, нужно найти проекцию тензора напряжений σ, вычисленного в точке  , на направление нормали
, на направление нормали 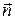 . Тензор напряжений σ в точке
. Тензор напряжений σ в точке  определяет напряженное состояние сплошной среды в этой точке.
определяет напряженное состояние сплошной среды в этой точке.
Докажем, что девять компонент 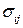 образуют тензор 2-го ранга, т.е.
образуют тензор 2-го ранга, т.е.
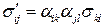 .
.
Для этого рассмотрим вектор напряжений на произвольной площадке с нормалью 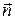 . Вектор является инвариантом, следовательно,
. Вектор является инвариантом, следовательно,
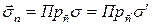 ,
,
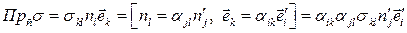 ,
,
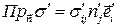 .
.
Тогда
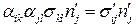 ,
, 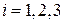
или
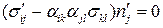 ,
, 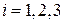 .
.
Так как 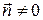 , то
, то
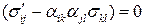 ,
, 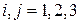 .
.
Что и требовалось доказать.
Дата добавления: 2015-12-29; просмотров: 5785;
