Закон сохранения момента количества движения
В теоретической механике момент количества движения материальной точки  массы
массы 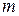 относительно точки
относительно точки 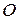 , начала некоторой инерциальной системы координат, определяется как
, начала некоторой инерциальной системы координат, определяется как
 ,
,
где

Уравнение момента количества движения материальной точки имеет вид
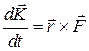 ,
,
где 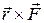 – момент главного вектора действующих на нее сил относительно точки
– момент главного вектора действующих на нее сил относительно точки 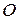 .
.
Момент количества движения системы материальных точек  относительно точки
относительно точки 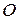
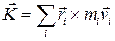 ,
,
где
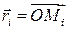 .
.
Уравнение момента количества движения системы материальных точек имеет вид
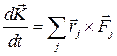 ,
,
причем в силу третьего закона Ньютона в сумме учитываются моменты только внешних по отношению к системе сил, то есть производная по времени от момента количества движения системы точек относительно некоторой точки 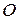 равняется сумме моментов всех внешних действующих на систему сил относительно той же точки
равняется сумме моментов всех внешних действующих на систему сил относительно той же точки 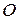 .
.
Получим уравнение моментов количества движения сплошной среды. Рассмотрим произвольный материальный объем 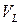 с поверхностью
с поверхностью 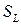 . Моментом количества движения объема
. Моментом количества движения объема 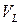 сплошной среды относительно точки
сплошной среды относительно точки 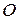 называется вектор
называется вектор
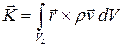 ,
,
где 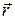 – радиус-вектор материальной точки объема
– радиус-вектор материальной точки объема 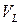 относительно точки
относительно точки 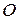 , а
, а 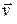 ,
, 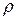 – скорость и плотность частицы сплошной среды.
– скорость и плотность частицы сплошной среды.
Согласно закону сохранения момента количества движения скорость изменения момента количества движения материального объема 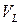 равна сумме моментов действующих на этот объем внешних массовых и поверхностных сил
равна сумме моментов действующих на этот объем внешних массовых и поверхностных сил
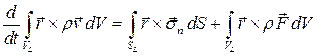 .
.
Уравнение можно записать и для контрольного объема 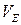 аналогично тому, как это было сделано в случае закона сохранения количества движения.
аналогично тому, как это было сделано в случае закона сохранения количества движения.
Преобразуем уравнение , используя полученные выше формулу дифференцирования интеграла и обобщенную формулу Гаусса-Остроградского
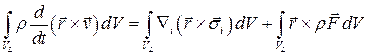
В силу произвольности объема 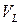 и согласно теореме 1 параграфа 1.7.1 получим дифференциальное уравнение баланса момента количества движения
и согласно теореме 1 параграфа 1.7.1 получим дифференциальное уравнение баланса момента количества движения
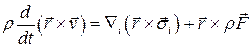 .
.
Теорема. Тензор напряжений является симметричным тензором 2-го ранга.
◄ Из уравнения количества движения
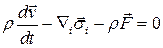 ,
,
следует равенство
 ,
,
или
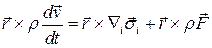 .
.
Вычтем это уравнение из уравнения моментов количества движения, переписанного в виде
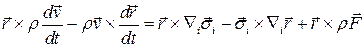 .
.
Получим
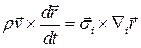 .
.
Так как 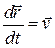 и
и 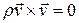 , то из последнего равенства следует, что
, то из последнего равенства следует, что
 .
.
Вычислим частную производную от радиус-вектора
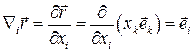 .
.
Тогда
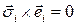
или
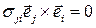 .
.
Разобьем сумму 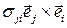 на два слагаемых:
на два слагаемых:
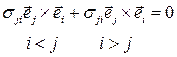 .
.
В первом слагаемом сгруппированы все члены с индексами 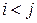 , во втором –
, во втором – 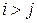 . Во втором слагаемом можем обозначить индекс
. Во втором слагаемом можем обозначить индекс 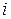 как
как 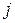 , а
, а 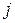 как
как 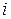 , так как сумма не зависит от обозначения индекса суммирования
, так как сумма не зависит от обозначения индекса суммирования
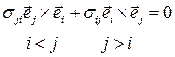 .
.
Поменяем порядок сомножителей во втором слагаемом
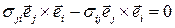 ,
,
и вынесем общий множитель за скобку
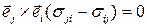 ,
, 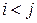 .
.
Расписав сумму слева почленно для 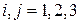 (
( 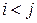 ) и вычислив векторные произведения базисных векторов, можно убедиться, что
) и вычислив векторные произведения базисных векторов, можно убедиться, что
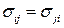 . ►
. ►
Замечание. Тензор напряжений является симметричным для многих сред, такой случай называется классическим. Но для некоторых структурированных сред с внутренними напряжениями он может быть несимметричным из-за наличия внутренних моментов, а также моментов распределенных массовых и поверхностных пар сил.
Дата добавления: 2015-12-29; просмотров: 1083;
