Уравнение внутренней энергии

Уравнение внутренней энергии получается путем вычитания из уравнения полной энергии уравнения кинетической энергии . Оно имеет вид

.

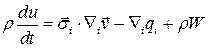Часть полной работы поверхностных сил отвечает за изменение кинетической энергии – 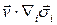, другая часть – за изменение внутренней энергии.

Выясним физический смысл первого слагаемого справа. Для этого покажем, что

,

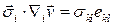то есть свертка тензоров напряжений и скоростей деформаций.

Действительно,

,

.

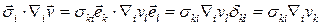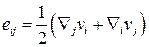В частности,

,

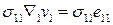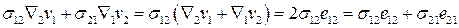
в силу симметричности тензоров напряжений и скоростей деформаций.

Аналогичные соотношения можно получить и для других значений индексов суммирования. Суммируя по всем значениям 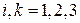, получим искомую свертку.

Дифференциальное уравнение справедливо для внутренней материальной частицы сплошной среды. Поэтому свертку тензоров напряжений и скоростей деформаций можно интерпретировать как мощность внутренних поверхностных сил на деформациях в единице объема. Таким образом, в уравнении внутренней энергии содержится внутренний источник энергии за счет процессов взаимодействия между частицами среды, что принципиально отличает его от уравнений неразрывности, импульса, момента импульса.

Итак, уравнение внутренней энергии может быть записано и в такой форме

.

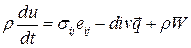Заметим, что если

, , ,

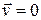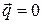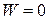то

,

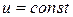т.е. внутренняя энергия неподвижной теплоизолированной среды неизменна.