Потенциальное течение идеальной несжимаемой жидкости в поле внешних потенциальных сил

Пусть внешние массовые силы имеют потенциал 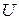, тогда .

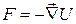Запишем уравнение импульсов

.

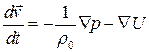В этом случае удобно воспользоваться формулой Громеки-Ламба

.

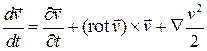Так как течение потенциальное, то

.

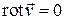Тогда уравнение импульсов примет вид

.

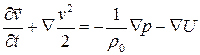Выразим скорость через потенциал

.

В первом слагаемом поменяем порядок дифференцирования, тогда

.

Интегрируя по пространству, получим

.

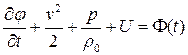Это решение называется интегралом Коши-Лагранжа.

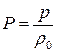Интеграл Коши-Лагранжа можно получить и для баротропной сжимаемой жидкости. В этом случае в уравнение импульсов следует ввести функцию давления P, используя равенство . В частности, для несжимаемой жидкости , а для адиабатического течения совершенного газа .

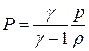Запишем интеграл Коши-Лагранжа для адиабатического течения совершенного газа при отсутствии массовых сил. В этом случае 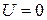, квадрат скорости звука равен 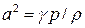, и интеграл принимает вид

.

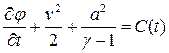Пусть в бесконечно удаленной точке

, , .

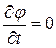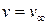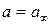Тогда

.

Интеграл Бернулли

Рассмотрим установившееся движение идеальной баротропной жидкости в потенциальном поле массовых сил. Запишем уравнение импульсов в форме Громеки-Ламба

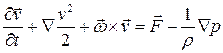
Учитывая стационарность течения, потенциальность массовых сил и функцию давления, получим

.

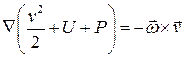Пусть 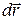– вектор элементарного перемещения частицы жидкости и

,

тогда

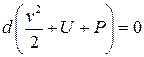
Отсюда следует интеграл Бернулли

.

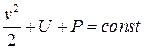Интеграл Бернулли имеет место, когда выполняется условие , т.е.

1) вдоль линии тока (траектории), когда ,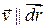

2) вдоль вихревой линии, когда ,

3) при безвихревом (потенциальном) движении, когда ,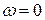

4) при винтовом движении, когда .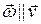

Заметим, что в случаях 1, 2 постоянная в интеграле Бернулли может быть своя для каждой траектории или вихревой линии, а в случаях 3, 4 она одна и та же для всего течения. Интеграл Бернулли в этих случаях следует непосредственно из .

Рассмотрим частные случаи.

А. Течение однородной несжимаемой жидкости в поле силы тяжести.

В этом случае 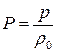, . Интеграл Бернулли принимает вид

.

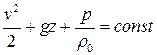Б. Адиабатическое течение совершенного газа при отсутствии массовых сил. В этом случае

.

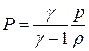Интеграл Бернулли принимает вид

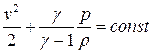
Заметим, что скорость звука в рассматриваемом случае равна

,

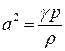поэтому

.

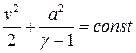Пусть скорость звука в покоящемся газе равна 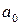, тогда

.

Отсюда видно, что скорость 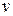ограничена и достигает максимума при

.

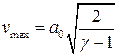Скорость потока равная местной скорости звука называется критической. Она равна

.

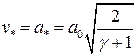Рассмотрим одномерное стационарное адиабатическое течение совершенного газа в трубке тока (Рис. 3.1.2).

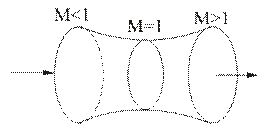Рис. 3.1.2.

Уравнение сохранения массы можно записать в виде ,

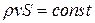где 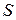– площадь поперечного сечения трубки тока. Логарифмируя и дифференцируя соотношение , получим

.

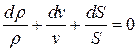Продифференцируем интеграл Бернулли и учтем, что

получим

.

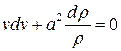Исключая плотность 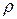из , и вводя число Маха 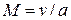, получим

.

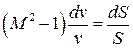Отсюда следует, что при дозвуковом течении ( ) уменьшение ( 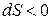) площади сечения приводит к увеличению скорости течения ( 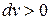). Но в сверхзвуковом течении ( 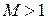) для увеличения скорости нужно увеличивать сечение 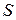. На этом принципе построено сопло Лаваля, в котором поток газа разгоняется от дозвуковой до сверхзвуковой скорости.