Упругое и линейно упругое изотропное тело
Сплошная среда называется упругим телом, если тензор напряжений является функцией тензора деформаций:
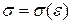 .
.
Если зависимость 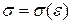 линейна, т.е.
линейна, т.е. 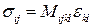 , то тело называется линейно упругим.
, то тело называется линейно упругим.
Если тензор коэффициентов упругости является изотропнымM´=M, то сплошная среда называется изотропным линейно упругим телом или кратко телом Гука.
Так же, как для ньютоновской жидкости , тензор M может быть записан в виде
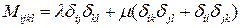 .
.
Подставив это выражение для 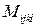 в выражение для
в выражение для 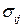 , получим уравнение состояния тела Гука или обобщенный закон Гука
, получим уравнение состояния тела Гука или обобщенный закон Гука
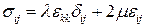 .
.
Коэффициенты 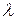 и
и 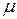 называются коэффициентами Ляме или модулями упругости. Латинское слово modulus переводится как мера.
называются коэффициентами Ляме или модулями упругости. Латинское слово modulus переводится как мера.
Аналогично теореме о главных осях тензоров напряжений и скоростей деформаций в ньютоновской жидкости можно доказать следующую теорему, при этом надо использовать обобщенный закон Гука.
Теорема. Для тела Гука главные оси тензоров напряжений и деформаций совпадают.
Уравнение импульсов для тела Гука, называемое уравнением Ляме, можно получить аналогично уравнениям Навье-Стокса. При этом предполагается, что деформации малые и тензор деформаций берется в виде
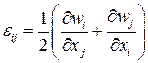 .
.
Тогда уравнение Ляме имеет вид
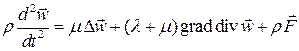 .
.
Рассмотрим три важных случая деформации твердого тела: растяжение стержня, всестороннее сжатие и сдвиг.
1. Растяжение стержня (Рис. 3.2.1) является примером одноосного напряженного состояния тела, описываемого тензором напряжений, имеющим в главных осях следующий вид
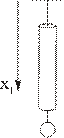 Рис. 3.2.1
Рис. 3.2.1
| 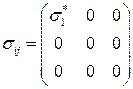
|
Запишем выражения для диагональных компонент тензора напряжений в соответствии с обобщенным законом Гука
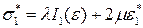 ,
,
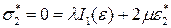 ,
,
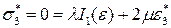 .
.
Последние два равенства запишем более подробно
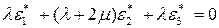 ,
,
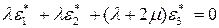 .
.
Вычтем из первого уравнения второе, получим
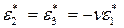 ,
,
где
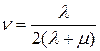
– коэффициент Пуассона.
Подставим найденные значения в выражение для 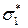 , получим
, получим
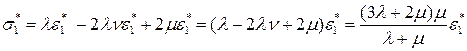 .
.
Таким образом, для растяжения стержня связь между продольным напряжением и деформацией (закон Гука) имеет вид
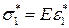 ,
,
где коэффициент
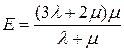
называется модулем Юнга.
Поперечные и продольные деформации связаны соотношением
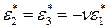 .
.
Дата добавления: 2015-12-29; просмотров: 3918;
