Ньютоновская жидкость

Сплошная среда называется вязкой жидкостью, если тензор напряжений является функцией тензора скоростей деформаций

.

Рассмотрим частный случай линейно-вязкой жидкости, когда эта функция является линейной

,

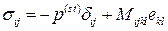где 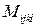– постоянный тензор, компоненты которого называются коэффициентами вязкости, 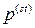– давление покоя или гидростатическое давление. В неподвижной жидкости

.

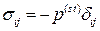Ранее в параграфе 2.4.2 было введено представление тензора напряжений в виде

,

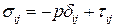где 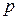– давление .

Вообще говоря,

.

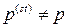Тензор четвертого ранга M имеет 81 компоненту. Учитывая симметричность тензора напряжений и тензора скоростей деформаций, можно показать, что у тензора M независимых компонент 36. Число независимых компонент значительно уменьшается в случае, когда тензор M является изотропным M´=M. Жидкость в этом случае также называется изотропной.

Рассмотрим подробнее линейно-вязкие изотропные жидкости. Кратко такие жидкости называются ньютоновскими жидкостями.

Теорема. Для ньютоновской жидкости тензор M имеет следующий вид

.

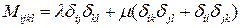Теорему примем без доказательства.

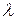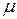Коэффициенты и называются коэффициентами Ляме.

Подставив выражение для 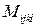в выражение для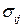

,

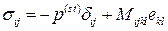получим уравнение состояния или реологическое уравнение ньютоновской жидкости

.

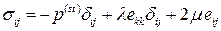Найдем давление 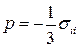. Проделав вычисления, получим

,

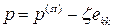где

.

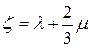Отсюда следует, что 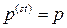при 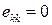, а это выполняется в двух случаях:

1) жидкость находится в состоянии покоя, ;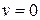

2) жидкость является несжимаемой.

Поэтому 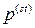и назвали гидростатическим давлением. Коэффициент 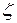называется коэффициентом объемной вязкости потому, что он стоит перед 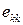, равным скорости относительного изменения объема жидкой частицы, и характеризует сопротивление жидкости изменению ее объема (сжатию).

Выразим уравнение состояния через давление p и девиатор тензора напряжений 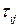. Получим

,

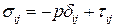где

.

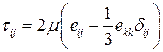Для несжимаемой жидкости

.

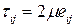Чтобы выяснить смысл этой формулы и коэффициента 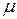, рассмотрим плоское слоистое (ламинарное) течение несжимаемой жидкости вдоль оси 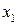(Рис. 3.1.3).

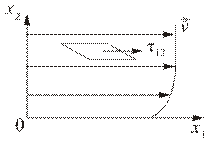Рис. 3.1.3

В этом случае вектор скорости имеет одну ненулевую компоненту 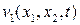, а девиатор – одно ненулевое касательное напряжение

.

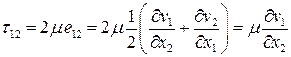Отсюда видно, что если скорости соседних слоев жидкости различаются 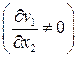, то между ними возникает трение, вызывающее и касательное напряжение. Такое свойство жидкости называют внутренним трением или вязкостью по Ньютону, а коэффициент 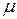- динамическим коэффициентом вязкости. Закон вязкого течения был предложен Ньютоном в виде

.

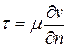Запишем выражение реологического закона для ньютоновской несжимаемой жидкости через давление и скорость (величины, которые можно измерить).

Тензор напряжений имеет три главные оси, тензор скоростей деформаций тоже. Возникает вопрос, совпадают ли указанные оси или нет. Ответ дает следующая теорема.

Теорема. Для ньютоновской жидкости главные оси тензора напряжений и тензора скоростей деформаций совпадают.

◄ Пусть тензор напряжений приведен к главным осям, т.е. 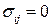, 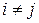. Из уравнения состояния для ньютоновской жидкости

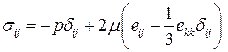
видно, что при .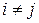

Обратно, пусть , 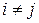. Из того же уравнения следует , . ►

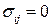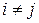Вязкой жидкостисвойственнадиссипация (рассеивание) механической энергии: за счет внутреннего трения часть кинетической энергии переходит в тепло и другие виды энергии. Чтобы убедиться в этом, рассмотрим уравнение притока тепла:

.

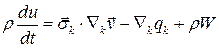Преобразуем выражение

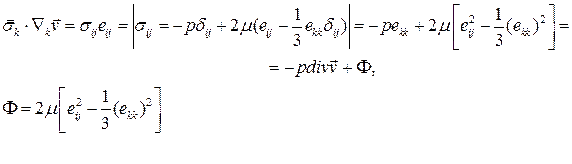
Функция 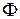называется диссипативной функцией. Пусть жидкость несжимаемая, 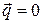, , 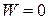тогда

, .

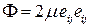Видно, что 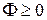.Следовательно, при движении вязкой жидкости происходит ее нагрев за счет диссипации кинетической энергии.

Как уже отмечалось, балансовые уравнения в дифференциальной форме справедливы для внутренних материальных частиц сплошной среды. Для пограничных частиц должны выполняться граничные условия.Рассмотрим два вида границ: поверхность твердого тела и поверхность раздела двух жидких сред.