Прямолинейное равноускоренное движение
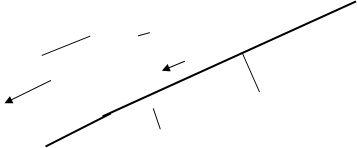
Рассмотрим наиболее общий случай прямолинейного равноускоренного движения – перемещение сосуда с жидкостью призматической формы по наклонной плоскости (рис.10).
z
 |



 ΔH a
ΔH a














 H
H
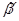 | 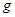 | ||


















 | 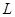 | ||

 x
x
Рис.10
Поведение жидкости будем исследовать в системе координат, скрепленной с сосудом. Плотность распределения силы тяжести, как и ранее, равна по значению g, а силы инерции – ускорению движения a (на рисунке сосуд движется вниз). Проекции равнодействующей плотностей на оси координат составляют
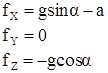 .
.
Подстановка в уравнение поверхности равного давления (5) и интегрирование дают
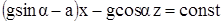 .
.
Отсюда видно, что поверхности равного давления представляют собой плоcкости, параллельные оси y и наклоненные к оси x под углом
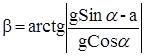 .
.
Угол наклона этих поверхностей к горизонту составляет
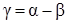 .
.
Положение свободной поверхности жидкости определяется координатой
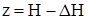 .
.
Как видно из рис. 10,
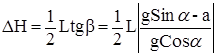 ,
,
где L – длина сосуда.
Расстояние H соответствует положению центра тяжести свободной поверх-ности жидкости в неподвижном сосуде, расположенном на наклонной плос-кости (показана штриховой линией). Оно совпадает с отметкой уровня жид-кости над дном сосуда, перенесенного на горизонтальную плоскость. Уравнение для расчета давления в жидкости получим с использованием уравнения (4), которое после подстановки и интегрирования дает
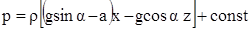 .
.
Константу интегрирования найдем из граничного условия:
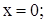
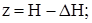
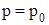 .
.
Окончательно получим
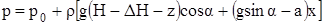
В частности, для задней стенки сосуда 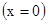 :
:
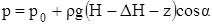 ,
,
передней стенки 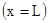
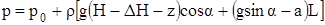 ,
,
дна 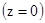
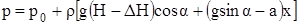 .
.
Силы давления на стенки сосуда, как известно, равны произведению давления в центре тяжести смоченной поверхности на ее площадь. Коорди-наты центров давления, рассчитанные по описанной в разделе 7 методике, для задней и передней стенок сосуда составляют
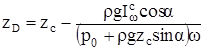 ,
,
где 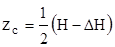 – координата центра тяжести смоченной поверхности задней стенки;
– координата центра тяжести смоченной поверхности задней стенки;
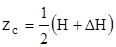 – то же для передней стенки.
– то же для передней стенки.
Частными случаями равноускоренного движения сосуда с жидкостью являются перемещения в вертикальном и горизонтальном направлениях. Расчетные соотношения легко получаются подстановкой в приведенные выше выражения соответственно a = 90º и 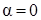 º. Особо отметим, что при падении сосуда с ускорением, равным ускорению свободного падения, "весовое" давление компенсируется “инерционным”, и жидкость ведет себя, как в невесомости, т.е. давление во всех ее точках равно внешнему давлению.
º. Особо отметим, что при падении сосуда с ускорением, равным ускорению свободного падения, "весовое" давление компенсируется “инерционным”, и жидкость ведет себя, как в невесомости, т.е. давление во всех ее точках равно внешнему давлению.
Дата добавления: 2015-11-26; просмотров: 1118;
