Сила гидростатического давления на плоскую поверхность и точка ее приложения
Для проведения прочностных расчетов резервуаров, сосудов под давле-нием и разнообразных гидротехнических устройств необходимо знать равно-действующую силу гидростатического давления жидкости на стенку и точку ее приложения. Эти данные можно получить с использованием известных положений теоретической механики.
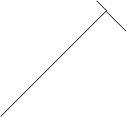
Рассмотрим плоскую поверхность произвольной формы (рис.5), подвер-гающуюся одностороннему давлению жидкости.
 |

















 p0 l
p0 l






 ld lc h
ld lc h









 dω hc hd
dω hc hd




 C H
C H
 | |||
 | |||


 D
D


 α
α
 | |||
 | |||
Рис.5
Поверхность наклонена под углом α к горизонту и перпендикулярна плос-кости чертежа. В соответствии с уравнением (7) эпюра распределения дав-ления на поверхность имеет вид трапеции с основаниями, соответствующими внешнему давлению 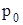 и суммарному давлению на глубине H, дополнительно включающему “весовое” давление
и суммарному давлению на глубине H, дополнительно включающему “весовое” давление 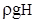 . На элементарную площадкуdω, расположенную на глубине h, действует сила
. На элементарную площадкуdω, расположенную на глубине h, действует сила
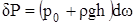
Интегрирование по всей поверхности дает значение искомой силы давления
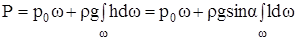
Интеграл 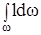 представляет собой статический момент рассматриваемой поверхности относительно линии пересечения плоскости, в которой она рас-положена, с уровнем жидкости. Как известно, этот момент равен произве-дению площади поверхности на расстояние
представляет собой статический момент рассматриваемой поверхности относительно линии пересечения плоскости, в которой она рас-положена, с уровнем жидкости. Как известно, этот момент равен произве-дению площади поверхности на расстояние 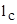 до центра тяжести C. После подстановки получим
до центра тяжести C. После подстановки получим
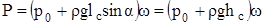
Таким образом, равнодействующая сила гидростатического давления на плоскую поверхность направлена по нормали к этой поверхности и равна произведению давления в ее центре тяжести на площадь.
Расстояние до точки приложения силы давления, называемой центром давления D, можно найти из условия, что момент равнодействующей силы относительно указанной выше оси равен сумме моментов составляющих

Отсюда
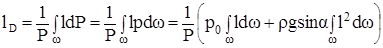
Смысл и способ вычисления первого интеграла уже известны. Второй интеграл 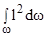 представляет собой момент инерции рассматриваемой поверх-ности. В теоретической механике показывается, что он равен сумме цент-рального момента инерции, т.е. момента относительно оси, проходящей через центр тяжести параллельно выбранной, и произведения квадрата расстояния до центра тяжести на площадь поверхности
представляет собой момент инерции рассматриваемой поверх-ности. В теоретической механике показывается, что он равен сумме цент-рального момента инерции, т.е. момента относительно оси, проходящей через центр тяжести параллельно выбранной, и произведения квадрата расстояния до центра тяжести на площадь поверхности
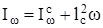
После подстановки получим
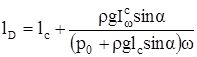
Глубина погружения центра давления, равна
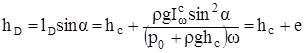
Как видно, центр давления расположен ниже центра тяжести на величину e, называемую эксцентриситетом. Физически это объясняется возрастанием гидростатического давления с глубиной погружения. При заданных форме и размерах фигуры эксцентриситет зависит от угла α, заглубления центра тяжести и давления на свободной поверхности. Максимальное смещение наблюдается при касании кромкой фигуры поверхности жидкости и 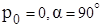 . Для горизонтальных плоских фигур
. Для горизонтальных плоских фигур 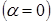 центры тяжести и давления совпадают. Моменты инерции некоторых фигур, необходимые для проведения инженерных расчетов, приведены на рис.6.
центры тяжести и давления совпадают. Моменты инерции некоторых фигур, необходимые для проведения инженерных расчетов, приведены на рис.6.











 h hb³/12 h hb³/32
h hb³/12 h hb³/32
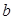 | 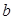 | ||||
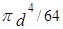 | |||||
 |  |  |  |




 Рис.6
Рис.6
Дата добавления: 2015-11-26; просмотров: 1331;
