Основное уравнение гидростатики и закон Паскаля
В большинстве прикладных задач равновесие жидкости рассматривают в поле одной массовой силы, а именно, силы тяжести. В этом случае проекции 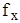 и
и 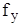 равны нулю, а проекция
равны нулю, а проекция 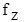 при указанной на рис.2 ориентации осей координат отрицательна и численно равна ускорению свободного падения. При этих условиях уравнения Эйлера приобретают вид
при указанной на рис.2 ориентации осей координат отрицательна и численно равна ускорению свободного падения. При этих условиях уравнения Эйлера приобретают вид
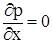 ,
, 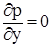 ,
, 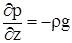
Первые два из них показывают, что в горизонтальных направлениях давление не меняется, т.е. все горизонтальные сечения жидкости являются поверхностями равного давления. Третье уравнение характеризует изменение гидростатического давления в вертикальном направлении. Для несжимаемой жидкости  интегрированием получаем
интегрированием получаем
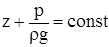
или с использованием условий на свободной поверхности 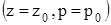
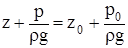 (6)
(6)
Соотношение (6) носит название основного уравнения гидростатики. Оно имеет следующий геометрический смысл: гидростатический напор 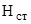 , представляющий собой сумму геометрической z и пьезометрической
, представляющий собой сумму геометрической z и пьезометрической 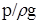 высот, во всех точках покоящейся жидкости одинаков.
высот, во всех точках покоящейся жидкости одинаков.
Наглядное представление об указанном свойстве гидростатического напора можно получить в опыте с откачанными стеклянными трубками (пьезометрами), присоединёнными открытыми концами к точкам 1 и 2 резервуара с жидкостью (рис. 3).









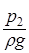 |








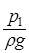 | 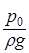 |



 P P
P P























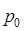 |











 1 2 z2 z0
1 2 z2 z0
z1


 0 0
0 0
Рис.3
Так как высота подъёма жидкости в пьезометре над уровнем жидкости в резервуаре определяется давлением 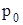 на её свободную поверхность, то уровни в обоих пьезометрах установятся на одинаковом расстоянии
на её свободную поверхность, то уровни в обоих пьезометрах установятся на одинаковом расстоянии 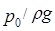 от этой поверхности и, следовательно, от плоскости сравнения 0-0.
от этой поверхности и, следовательно, от плоскости сравнения 0-0.
Последнее расстояние, как легко видеть, совпадает с величиной гидростатического напора. Горизонтальная плоскость, проходящая через уровни жидкости в пьезометрах, называется пьезометрической, а её пересечение с плоскостью чертежа – пьезометрической линией Р-Р.
После умножения всех членов на ускорение свободного падения уравне-ние (6) приобретает смысл закона сохранения энергии в гидростатике – полная удельная потенциальная энергия покоящейся жидкости, равная сумме энергии положения и энергии давления, есть величина постоянная
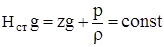
Основное уравнение гидростатики можно преобразовать к виду
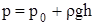 , (7)
, (7)
где 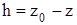 – заглубление рассматриваемой точки относительно cвободной поверхности жидкости.
– заглубление рассматриваемой точки относительно cвободной поверхности жидкости.
Из соотношения (7) следует, что давление в данной точке покоящейся жидкости равно сумме внешнего давления 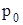 , действующего на свободную поверхность, и “весового” давления
, действующего на свободную поверхность, и “весового” давления 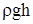 , создаваемого столбом жидкости, расположенной над этой точкой.
, создаваемого столбом жидкости, расположенной над этой точкой.
Уравнение (7) отражает также так называемое свойство идеальной “проводимости” жидкости, составляющее содержание закона Паскаля: давление, приложенное к внешней поверхности, передается во все точки жидкости без изменения.
На законе Паскаля основано действие многих гидравлических машин: прессов, подъемников, тормозов, мультипликаторов и др. Принципиальная схема гидравлического пресса показана на рис. 4.
 P1
P1
 | ||||||
 | ||||||
 | ||||||
 | ||||||




 П1 h П2
П1 h П2
 | |||||||
 | |||||||
 |  | ||||||






 P2
P2
 |  |
Рис.4
К поршню 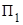 приложена внешняя сила
приложена внешняя сила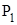 ,создающая в жидкости избыточное гидростатическое давление
,создающая в жидкости избыточное гидростатическое давление
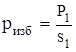 ,
,
где 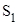 – площадь поперечного сечения первого поршня.
– площадь поперечного сечения первого поршня.
Это давление вместе с дополнительным “весовым” давлением столба жидкости высотой h действует на второй поршень 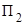 с площадью поперечного сечения
с площадью поперечного сечения 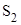 , создавая сжимающее усилие
, создавая сжимающее усилие
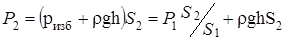 .
.
Таким образом, гидравлический пресс позволяет увеличить силу на выходе примерно в 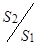 раз.
раз.
Дата добавления: 2015-11-26; просмотров: 2078;
