Гидростатическое давление и его свойства

Гидростатическое давление совпадает с нормальным напряжением в покоящейся жидкости 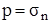. Оно обладает следующими свойствами:

1) действует нормально к площадке, имеющей центром рассмат-риваемую точку (по определению), и является сжимающим;

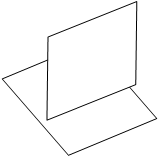
2) не зависит от ориентации этой площадки в пространстве (рис. 1).

Рис. 1

Исторически сложились две системы отсчёта давления: от нуля и атмо-сферного давления. В первой системе оно называется абсолютным и обозна-чается p, а во второй в зависимости от величины – избыточным 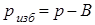или вакуумметрическим 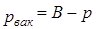, где B – атмосферное давление. Для измерения атмосферного давления в 1643 г Торичелли первым использовал ртутный барометр.

При проведении прочностных расчётов сосудов и устройств под давлением удобно пользоваться второй системой отсчёта, так как в таких задачах принимается во внимание только неуравновешенная часть давления.

Давление измеряют в н/м², Па, кПа, МПа, барах, технических и физических атмосферах, мм рт.ст. Связь между единицами измерения давле-ния такова: 1н/м² = 1Па; 1 кПа = 100Па; 1 МПа = 10⁶ Па; 1бар = 10⁵ Па;

1 ат = 0,9808 бар; 1 атм = 1,0133 бар; 1 мм рт. ст. = 133,3 Па.

Дифференциальные уравнения равновесия жидкости
(уравнения Эйлера в гидростатике)

Гидростатическое давление в жидкости, подверженной действию внеш-них сил, в общем случае зависит от их величины и координат рассматриваемой точки. Для установления этой зависимости выделим в покоящейся жидкости элементарный параллелепипед со сторонами 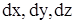(рис. 2).

z

δPx΄ δPx΄΄

dz

dx dy

y x

Рис.2

К граням параллелепипеда приложим нормальные сжимающие поверх-ностные силы 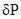,замещающие воздействие окружающей среды, и учтем наличие некоторой массовой силы .

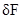Условием равновесия параллелепипеда является равенство нулю алге-браической суммы проекций всех сил на каждую ось. Применительно к оси x

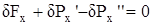
Выражая массовую силу через плотность ее распределения

,

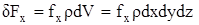а поверхностные силы через давление в центре параллелепипеда

,

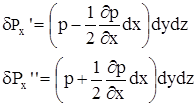после подстановки, приведения подобных членов и деления на массу параллелепипеда получим

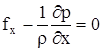(1)

Условия равновесия в проекциях на оси y и z аналогичны

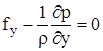(2)

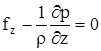(3)

Уравнения (1) – (3) в частных производных получены Эйлером в 1755 г. и носят его имя. Они характеризуют влияние массовых сил и плотности жидкости на изменение гидростатического давления.

При отсутствии массовых сил, например в невесомости, давление во всех точках покоящейся жидкости одинаково и равно давлению, приложенному на свободной поверхности.

После умножения уравнений (1) – (3) соответственно на 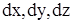и сло-жения получим

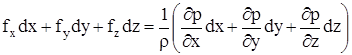
Выражение в скобках представляет собой полный дифференциал давления. С учетом этого условие равновесия жидкости можно записать в виде

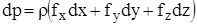(4)

Отсюда вытекает следующее уравнение поверхностей равного давления, вдоль которых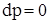

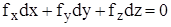(5)

Одной из них является свободная поверхность жидкости, все точки которой находятся под одинаковым внешним давлением.