Физические свойства и модели жидкостей

Объектом исследования в гидравлике является так называемая капельная жидкость, которую, имея в виду молекулярную структуру и физические свойства, обычно определяют как состояние вещества, промежуточное между твёрдым телом и газом. Для жидкости характерна достаточно плотная упаковка молекул и наличие динамического “ближнего порядка” в их расположении, что роднит её с твёрдым телом. В то же время квазиупорядоченные группы молекул относительно подвижны, что придаёт жидкости сходство с газом и внешне проявляется в таком свойстве как текучесть. На это сходство обратили внимание ещё Эндрюс и Ван-дер-Ваальс, авторы идеи о непрерывности перехода вещества из газообразного состояния в жидкое.

Поведение жидкостей в тех или иных условиях, описываемое законо-мерностями и зависимостями гидравлики, определяется их физическими свойствами и внешними воздействиями. К числу наиболее существенных свойств относят плотность, барическую и термическую сжимаемости, по-верхностное натяжение, вязкость.

Плотность жидкости определяют как отношение ее массы к занимаемому объему

.

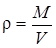Для воды при обычных условиях r =1000 кг/м³.Обратную величину плотности называют удельным объемом v.

Сжимаемость жидкости под действием внешних сил (барическая сжи-маемость) характеризуется коэффициентом объемного сжатия

,

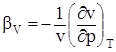где p– давление, Па;

Т – температура. Для воды 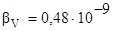1/Па.

Влияние температуры на объем жидкости (термическая сжимаемость) характеризуется температурным коэффициентом объемного расширения или сжатия

,

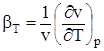который для воды равен 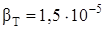1/К.

Силы межмолекулярного взаимодействия в поверхностном слое жидкости характеризуют коэффициентом поверхностного натяжения, численно равным силе, возникающей между двумя смежными площадками на свободной поверхности, если разделяющая их линия имеет единичную длину. Для воды этот коэффициент равен 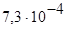Н/м.

Вызываемое этим натяжением искривление свободной поверхности в месте контакта жидкости с твердой поверхностью изменяет молекулярное давление на внутренние слои жидкости, что приводит к появлению капиллярных эффектов. Высота поднятия (смачиваемая поверхность) или снижения (несмачиваемая поверхность) уровня жидкости в капилляре помимо коэффициента поверхностного натяжения зависит от радиуса капилляра. В тонких полимерных структурах (глинистые грунты) вода может подниматься на несколько метров.

Способность слоев жидкости сопротивляться смещению называется вяз-костью. В движущейся жидкости возникают касательные напряжения, вели-чина которых зависит от прочности межмолекулярных связей и для норма-льных жидкостей выражается законом внутреннего трения Ньютона

; ,

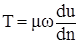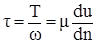где 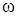– площадь смежных слоёв жидкости;

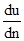– градиент скорости;

Т – сила трения.

Коэффициент динамической вязкости 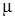численно равен напряжению на поверхности раздела смежных слоев жидкости при единичном градиенте скорости. Единицей динамической вязкости в системе СИ является Па∙с или пуазейль. Величину в десять раз меньшую называют пуазом. Для воды 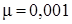Па·с.

В расчётах часто используют коэффициент кинематической вязкости

,

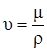имеющий размерность м²/с. Внесистемная единица 1 см²/с носит название стокс. С повышением температуры вязкость жидкостей уменьшается. Давление на значение 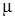практически не влияет.

Помимо нормальных или капельных жидкостей, существуют так назы-ваемые неньютоновские жидкости с аномальными вязкостными свойствами. Некоторые из них (бетон, асфальт, глина, тесто) оказывают сопротивление растягивающим усилиям, проявляют текучесть только под воздействием заметных сдвигающих сил и характеризуются наличием касательных напряжений даже в состоянии покоя. В других неньютоновских жидкостях нарушается линейная зависимость касательных напряжений от градиента скорости (эмульсии, суспензии, аэрированные жидкости).

В гидравлике для упрощения анализа широко применяют различные модели жидкостей, наделяемые лишь теми свойствами, которые существенны для рассматриваемых явлений. Как правило, жидкость считают сплошной несжимаемой средой с непрерывно изменяющимися характеристиками, что позволяет исследовать ее поведение с помощью дифференциальных уравнений. Учет сжимаемости необходим, когда природа явления связана с упругими деформациями среды (ударные волны в трубопроводах). В ряде случаев характер гидравлических явлений слабо зависит от вязкости. Их анализ удобно проводить с использованием модели идеальной жидкости, в которой полностью отсутствуют силы внутреннего трения и эффекты, обусловленные сжимаемостью. При необходимости теоретические результаты корректируют на основе экспериментальных данных.

В каждой конкретной ситуации выбранная модель жидкости должна обеспечивать получение максимально простыми средствами всей необходимой информации с достаточной для инженерных приложений точностью.