Теоремы сложения и умножения вероятностей.
Теоремы сложения вероятностей.
Теорема 1.Вероятность суммы двух несовместных событий равна сумме их вероятностей.
P (А+В) = P (А) + P (В)
Доказательство:
Пусть n‒общее число элементарных событий, в результате которых может произойти событие A или B. Пусть m‒число элементарных событий , благоприятствующих событию А, k‒число элементарных событий, благоприятствующих событию В.
Тогда событию A+B будет благоприятствовать (m+k) – элементарных событий.
Получим
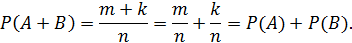
Следствие 1 .Сумма вероятностей противоположных событий равна единице.
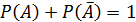
Доказательство: 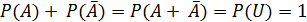
Следствие 2.Сумма вероятностей случайных событий, образующих полную группу, равна единице.
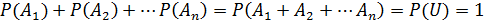
Распространим теорему 1 на любое число попарно несовместных событий.
Получим: 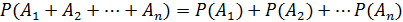
Теорема 2.
Вероятность суммы двух совместных событий равна сумме их вероятностей без вероятности их совместного осуществления.
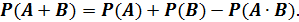
Доказательство:
Пусть n ‒ общее число элементарных событий, m ‒ число элементарных событий, благоприятствующих событию А, k ‒ число элементарных событий, благоприятствующих событию В.
Пусть среди (m+k) ‒ элементарных событий имеется l‒событий , благоприятствующих и событиюA и B одновременно.
Тогда событию A+B будет благоприятствовать (m+k‒ l) элементарных событий.
Следовательно, получим:
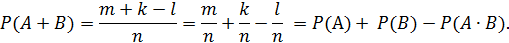
Пример 1.
Из колоды 36 карт, на удачу, достается одна.
Найти вероятность того, что вынутая карта или туз, или пиковой масти.
Решение:
Событие A ‒ вынутая карта туз.
Событие B ‒ вынутая карта пиковой масти.
A+B ‒ вынутая карта или туз, или пиковой масти, или пиковый туз.
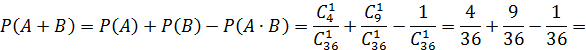
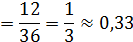
Дата добавления: 2015-12-16; просмотров: 1145;
