Классическое определение вероятности.

Вероятностью наступления события A называется число, равное отношению числа случаев, благоприятствующих событию A, к общему числу случаев (исходов, шансов или элементарных событий).

Вероятность (Р)

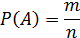
Где n‒общее число случаев, m‒ число случаев, благоприятствующих событию А.

Вероятность невозможного события:

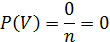
Вероятность достоверного события:

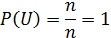
Вероятность случайного события:

0≤P(A)≤1

Статистической вероятностью событияA называется относительная частота появления события в n‒произведенных испытаниях.

Опытная (экспериментальная) вероятность:

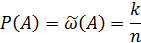
Следовательно, 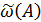–есть доля тех фактически произведённых испытаний, в которых событие A появилось. При 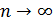,P(A)≈ (A)

Пример 1.

В коробке лежит 7 синих, 8 красных и 5 зеленых шаров.

Решение:

Событие A ‒ шар зеленый;

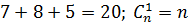
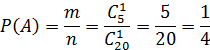
Пример 2.

В коробке лежат 100 электроламп, из них 5 испорченных (бракованных).

Решение:

Событие A ‒ на удачу, выбранные 2 электролампы исправны.

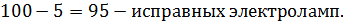
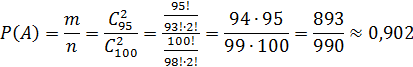
Пример3.

В коробке лежит 10 шаров: 6 белых и 4 черных.

Найти:

Вероятность того, что из пяти взятых наугад шаров будет 4 белых.

Решение:

Найдем число благоприятных исходов: число способов, которыми можно взять 4 белых шара из 6 имеющихся,равно

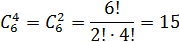
Общее число исходов определяется числом сочетаний из 10 по 5:

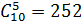
Искомая вероятность P = 15/252 ≈ 0,06.

Геометрическая вероятность, то есть вероятность попадания точки в некоторую область, отрезок, часть плоскости.

Геометрической вероятностью события Aназывают отношение меры области, благоприятствующей появлению события A, к мере всей области.

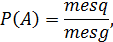
где mes ‒мера (длина, площадь, объём области).