Лекция 3.АЛГЕБРА СОБЫТИЙ.
Операции над случайными событиями.
Определение 1.Суммой двух событий A и B называется событие C, состоящее в осуществлении хотя бы одного из событий A или B.
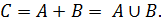
Возможны два случая:
1. Если A и B несовместны, тогда A+B означает, что произойдет или A, или В.
2. Если A и B совместны, тогда A+Bозначает, что произойдет илиA,или B, или A и B одновременно.
Определение 2.Произведением двух событий A и B называется событие C, состоящее в одновременном осуществлении событий A и B.
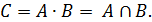
Пример 1.
Событие A‒ карта дама.
Событие B‒ карта пиковой масти.
Тогда, A + B ‒ вынутая карта или дама, или карта пиковой масти, или пиковая дама. A  B ‒ вынутая карта пиковая дама.
B ‒ вынутая карта пиковая дама.
Правило произведения событий.
Если какой ни будь объект A можно выбрать m‒ способами и после каждого такого выбора другой объект B можно выбрать k‒ способами, то пары объектов «A иBодновременно» можно выбрать m  k‒ способами.
k‒ способами.
Пример 2.
В лотереи из 50 билетов 8 выигрышных билетов.
Найти вероятность того, что среди первых 5‒ти наугад выбранных билетов 2 будут выигрышными.
Решение:
50 ‒ 8 = 42 ‒ билета невыигрышных.
Событие A ‒ среди первых 5‒ти билетов 2 выигрышных.
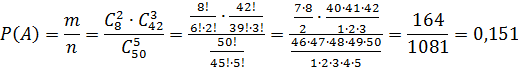
Пример3.
В ящике находится 10 стандартных и 5 нестандартных деталей.
Какова вероятность, что среди наугад взятых 6 деталей будет 4 стандартных и 2 нестандартных?
Решение:
Общее число исходов равно
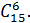
Число благоприятных исходов определяется произведением
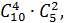
где первый сомножитель соответствует числу вариантов изъятия из ящика 4‒х стандартных деталей из 10, а второй ‒ числу вариантов изъятия из ящика 2‒х нестандартных деталей из пяти. Отсюда следует, что искомая вероятность равна
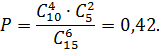
Дата добавления: 2015-12-16; просмотров: 2445;
