Виды дисперсий и закон сложения дисперсий

Наряду с изучением вариации признака по всей совокупности в целом часто бывает необходимо проследить количественные изменения признака по группам, на которые разделяется совокупность, а также между группами. Такое изучение вариации достигается посредством вычисления и анализа различных видов дисперсии.

Выделяют общую, межгрупповую и внутригрупповую дисперсии.

Общая дисперсия характеризует вариацию признака, которая зависит от всех условий в данной совокупности:

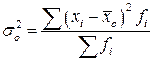, (5.16)

где 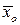- общая средняя для всей изучаемой совокупности.

Межгрупповая дисперсия отражает вариацию изучаемого признака, которая возникает под влиянием признака-фактора, положенного в основу группировки. Она характеризует колеблемость групповых (частных) средних 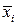около общей средней :

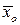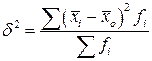, (5.17)

где 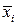- средняя по отдельным группам;

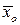- общая средняя;

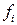- численность отдельных групп.

Средняя внутригрупповая дисперсия характеризует случайную вариацию в каждой группе. Эта вариация возникает под влиянием других неучитываемых факторов и не зависит от условия (признака-фактора), положенного в основу группировки:

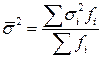. (5.18)

Существует закон, связывающий три вида дисперсии (правило сложения дисперсий):общая дисперсия равна сумме средней внутригрупповой дисперсии и межгрупповой дисперсии:

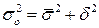. (5.19)

Очевидно, что чем больше доля межгрупповой дисперсии в общей дисперсии, тем сильнее влияние группировочного признака (например, квалификационного разряда) на изучаемый признак (количество изготовленных деталей).

Поэтому в статистическом анализе широко используется эмпирический коэффициент детерминации( ):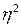

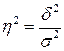. (5.20)

Эмпирический коэффициент детерминации показывает долю вариации результативного признака 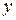под влиянием факторного признака 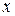(остальная часть общей вариации 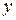обуславливается вариацией прочих факторов). При отсутствии связи эмпирический коэффициент равен нулю, а при функциональной связи - единице.

Например, если 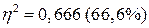, это значит, что на 66,6% вариация производительности труда рабочих обусловлена различиями в их квалификации и на 33,4% - влиянием прочих факторов.

Эмпирическое корреляционное отношение 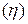– это корень квадратный из эмпирического коэффициента детерминации:

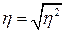. (5.21)

Оно показывает тесноту связи между группировочным и результативным признаками 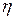, как и 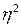, может принимать значения от 0 до 1.

Если связь отсутствует, то корреляционное отношение равно нулю, т.е. все групповые средние будут равны между собой, межгрупповой вариации не будет. Значит, группировочный признак никак не влияет на образование вариации.

Если связь функциональная, то корреляционное отношение будет равно единице. В этом случае, , т.е. внутригрупповой вариации не будет. Это означает, что группировочный признак целиком определяет вариацию изучаемого результативного признака.

Чем значение корреляционного отношения ближе к 1, тем теснее, ближе к функциональной зависимости связь между признаками.

Для качественной оценки тесноты связи на основе показателя эмпирического корреляционного отношения можно воспользоваться соотношением Чэддока:

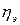
	0,1–0,3	0,3–0,5	0,5–0,7	0,7–0,9	0,9–0,99
Сила связи	слабая	умеренная	заметная	тесная	весьма тесная

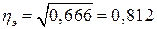, что свидетельствует о тесной связи между квалификацией рабочих и их производительностью труда.