Построение на чертеже натуральной величины отрезка прямой общего положения и углов наклона прямой к плоскостям проекций

Чтобы определить на эпюре истинную (натуральную) длину отрезка прямой, можно воспользоваться способом прямоугольного треугольника (рис.2.16, 2.1.7),

Прямая АВ - общего положения (то есть, не параллельна и не перпендикулярна ни одной из плоскостей проекций). Поэтому обе ее проекции А'В' и А"В" имеют искажения по сравнению с натуральными размерами.

На рис.2.16 слева, длина отрезка АВ и угол, составленный прямой АВ с плоскостью Н, определены из прямоугольного треугольника, построенного на проекцииА'В' при втором катете В'В°,равном В" 1.АВ=А'В°.

Для установления натуральной величины отрезка АВ проводим на одной из проекций (горизонтальной) прямую параллельную оси х.

Полученный отрезок А2 откладываем на перпендикулярно проведенном из точки А" отрезке и полученную точку А° соединяем с В". В результате построений получаем натуральную величину прямой АВ и угол j₂, который равен истинному углу наклона прямой АВ к плоскости V.

Отрезки линий уровня - фронтали, горизонтали, профильные проецируются в натуральную величину, соответственно на фронтальную, горизонтальную и профильные плоскости проекции. Во всех остальных случаях отрезки прямых проецируются с искажением.

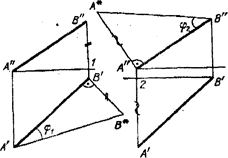
Рис.2.16 Рис.2.17

Угол прямой линии с плоскостью проекций определяется как острый угол между этой прямой и ее проекций на данную плоскость (рис. 2.17).

Этот угол входит в тот же прямоугольный треугольник, который строят для Н.В.

Если прямая имеет какую - либо проекцию, равную действительной ее длине, то на комплексном чертеже угол между проекцией этой прямой и плоскостью проекций будет действительным углом прямоугольного треугольника.