Параллельное проецирование. Центральное проецирование
МЕТОДЫ ПРОЕЦИРОВАНИЯ
Центральное проецирование
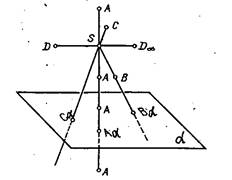 Центральное проецирование является наиболее общим случаем получения проекций геометрических фигур. Сущность метода центрального проецирования: пусть даны плоскость a и точка S, не принадлежащая плоскости a. Возьмем произвольную точку А, не принадлежащую плоскости a. Через заданную точку S и точку А проведем [SA) и отметим точку Аa, в которой этот луч пересекает плоскость a (рис.1.1.).
Центральное проецирование является наиболее общим случаем получения проекций геометрических фигур. Сущность метода центрального проецирования: пусть даны плоскость a и точка S, не принадлежащая плоскости a. Возьмем произвольную точку А, не принадлежащую плоскости a. Через заданную точку S и точку А проведем [SA) и отметим точку Аa, в которой этот луч пересекает плоскость a (рис.1.1.).
Плоскость a называют плоскостью проекции, точку S - центром проекции, полученную точку Аa - центральной проекцией точки А на плоскость a, [SАa) - проецирующим лучом.
|
Так как через две различные точки можно провести одну и только одну прямую, то можно сделать вывод, что при заданном аппарате проецирования каждая точка пространства будет иметь одну и только одну центральную проекцию. Обратное утверждение не имеет смысла.
 Для того, чтобы одноз-начно определить положение точки в пространстве, по ее центральным проекциям, необ-ходимо иметь две центральные проекции этой точки, получен-ные из двух различных центров S1 и S2 (рис.1.2.), можно определить положение точки А в пространстве. Для этого дос-таточно провести проеци-рующие лучи [S1Aa1) и [S2Aa2) и найти точку их пересечения.
Для того, чтобы одноз-начно определить положение точки в пространстве, по ее центральным проекциям, необ-ходимо иметь две центральные проекции этой точки, получен-ные из двух различных центров S1 и S2 (рис.1.2.), можно определить положение точки А в пространстве. Для этого дос-таточно провести проеци-рующие лучи [S1Aa1) и [S2Aa2) и найти точку их пересечения.
Параллельное проецирование
Параллельное проецирование - частный случай центрального проецирования. При параллельном проецировании центр проекции удален в бесконечность. В этом случае проецирующие лучи станут параллельны друг другу (рис.1.3.).
|
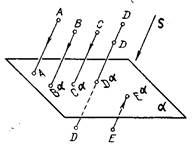 Полученные таким методом проекции называются параллельными. Аппарат параллельного проецирования определяется положением плоскости a и направлением проецирования S. Отмеченное ранее свойство центрального проецирования сохраняется и в данном случае. Формулируется оно следующим образом: каждая точка пространства, при заданном аппарате проецирования, будет иметь одну и только одну параллельную проекцию. Обратное утверждение не имеет смысла.
Полученные таким методом проекции называются параллельными. Аппарат параллельного проецирования определяется положением плоскости a и направлением проецирования S. Отмеченное ранее свойство центрального проецирования сохраняется и в данном случае. Формулируется оно следующим образом: каждая точка пространства, при заданном аппарате проецирования, будет иметь одну и только одну параллельную проекцию. Обратное утверждение не имеет смысла.
1.3. Основные инвариантные свойства параллельного
проецирования.
Геометрические фигуры, в общем случае, проецируются на плоскость проекции с искажением. В частности, при параллельном проецировании нарушаются метрические характеристики геометрических фигур (происходит искажение линейных и угловых величин). Но некоторые свойства оригинала сохраняются и на его проекции. Такие свойства называют инвариантными.
1.3.1. Проекция точки есть точка.
1.3.2. Проекция прямой на плоскость есть прямая.
1.3.3. Если в пространстве точка принадлежит линии, то проекция этой точки принадлежит проекции линии.
1.3.4. Проекции взаимно параллельных прямых также взаимно параллельны, а отношение отрезков таких прямых равно отношению их параллельных проекций.
1.3.5. Точка пересечения проекций пересекающихся прямых является точкой пересечения этих прямых.
1.3.6. Плоская фигура, параллельная плоскости проекции, проецируется на эту плоскость в конгруэнтную фигуру.
1.3.7. Плоский многоугольник в общем случае проецируется в многоугольник с тем же числом вершин.
1.3.8. Параллельный перенос оригинала или плоскости проекции не изменяет вида и размеров проекции оригинала.
Дата добавления: 2016-01-20; просмотров: 1435;
