Построение линии пересечения двух плоскостей. Две плоскости пересекаются по прямой линии, следовательно, в общем случае для построения линии пересечения двух плоскостей достаточно найти две точки

Две плоскости пересекаются по прямой линии, следовательно, в общем случае для построения линии пересечения двух плоскостей достаточно найти две точки, принадлежащие одновременно каждой из заданных плоскостей.

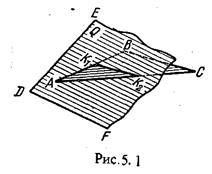
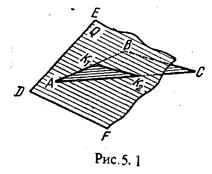
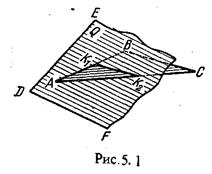На рис.5.1. такими точками являются К₁, К₂,

Выбор решения данной задачи зависит от расположения заданных плоскостей относительно плоскостей проекций.

Рассмотрим случай, когда хотя бы одна из пересекающихся плоскостей проецирующая. Рис.5.2, 5.3.

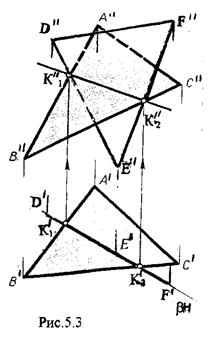
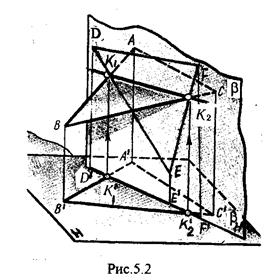
Даны плоскости a(АВС) и b(DEF), Плоскость b перпендикулярна к горизонтальной плоскости проекций, Так как треугольник DEF проецируется на плоскость Н в виде прямой линии (D¢F¢), то горизонтальная проекция l¢ линии пересечения плоскостей a и b совпадает с D¢F¢, Обозначаем на этой проекции K¢₁ и K¢₂, затем определяем K¢¢₁ и K¢¢₂ по условию их принадлежности к сторонам треугольника ABC K₁ÎAB, К₂ÎВС/

Рассмотрим общий случай построения линии пересечения двух плоскостей.

Способ построения линии пересечения двух плоскостей состоит в следующем (рис,5.4)

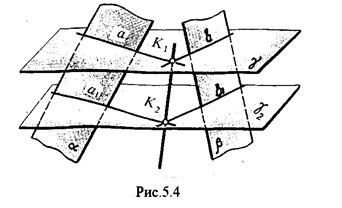
Заданные плоскости a и b пересекают третьей вспомогательной плоскостью g. Находим линии пересечения плоскости g с плоскостью a и плоскостью b

а= g Ç a ; b= g Ç b.

Точка k₁ определяется в пересечении а и b. Для того, чтобы найти точку К₂, проведем описанные построения еще раз с еще одной вспомогательной секущей плоскостью.

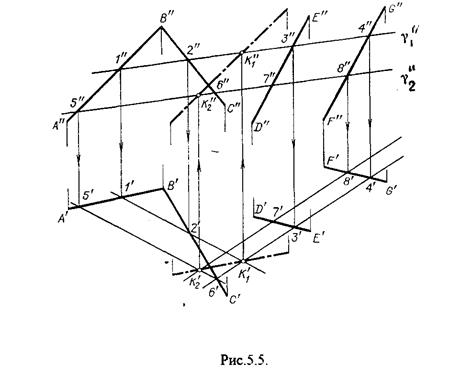
Рассмотрим как этот алгоритм реализуется на чертеже (рис.5.5.). Плоскость a задана двумя пересекающимися прямыми (АВ, ВС).

Плоскость b задана параллельными прямыми (ED, GF). Обе плоскости общего положения.

Проведем вспомогательную секущую плоскость g₁ перпендикулярную V и пересекающую каждую из плоскостей a и b.

При пересечении плоскости g₁ с плоскостью a получаем прямую «a₁» с проекциями 1²2², 1¢2¢, а при пересечении g₁ с b получаем прямую «b₁» с проекциями 3²4², 3¢4¢, Эти прямые расположенные в плоскости g₁ в своем пересечении определяют точку k₁ линии пересечения a и b.

K¢₁= 1¢2¢Ç3¢4¢ K¢¢₁ Îg²₁

Введя затем плоскость g₂ получим:

a₂ = g₂Ça с проекциями 5¢¢6¢¢, 5¢6¢

b₂= g₂Çb с проекциями 7²8², 7¢8¢

К₂= a₂ÇЬ₂

К¢₂=5¢6¢Ç7¢8¢

К¢¢₂ Îg²₂

Затем определяем проекции искомой линии пересечения K¢₁K¢₂ и K¢¢₁K¢¢₂.

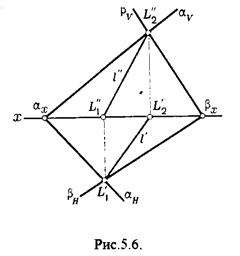
Если плоскости заданы их следами на плоскостях проекций, то точки, определяющую прямую пересечения плоскостей, находят на пересечение одноименных следов плоскостей.

L¢₁=a_H Ç b_H; L¢¢₁=a_V Ç b_V

В этом случае плоскости проекции выполняют роль вспомогательных секущих плоскостей, а соответствующие следы несут функции проекций прямых а¢, b¢ и а², b². (рис,5,6.).

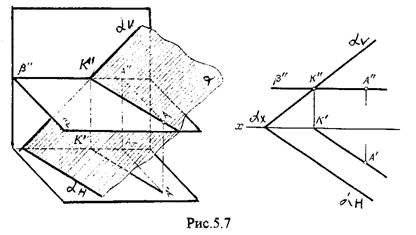
На рис.5.7. показан случай когда известно направление линии пересечения. Поэтому достаточно иметь лишь одну точку от пересечения следов и далее провести через эту точку прямую, исходя из положения плоскостей и их следов.

5.2. Пересечение прямой линии с плоскостью

Рассмотрим способы построения точки пересечения прямой с плоскостью при различном их расположении относительно плоскостей проекций.