Пересечение прямой линии с плоскостью перпендикулярной

К одной или двум плоскостям проекций.

Плоскость, перпендикулярная к плоскости проекций, проецируется на нее в виде прямой линии. На этой прямой должна находиться соответствующая проекция точки, в которой прямая пересекает плоскость.

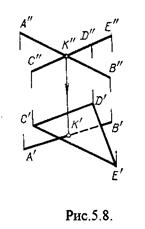
На рис,5,8 фронтальная проекция К точки пересечения прямой АВ с плоскостью a(CDE) определяется в пересечении проекций А²В² и С²Е², т.к. пл. a проецируется на пл. V в виде прямой линии. Определить проекцию К², находим К¢ по условию принадлежности на А¢В¢.

Т.к. прямая АВ в направлении от К к В находится под треугольником, часть ее горизонтальной проекции является невидимой и потому проведена штриховой линией.

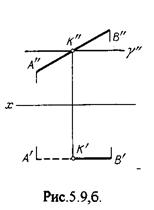
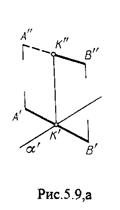
На рис.5.9а фронтальный след плоскости g является ее фронтальной проекцией. Проекция К² определяется в пересечении проекции А²В² и следа g² . Аналогично решается задача на рис.5.9.б.

Пересечение проецирующей прямой с плоскостью

Общего положения.

Прямая, перпендикулярная плоскости проекций проецируется на эту плоскость в точку. В эту же точку спроецируется искомая точка пересечения рис.5.10.

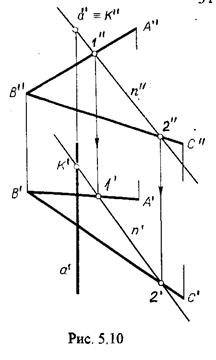Прямая а ^ V, К² сов-падает с а². Горизонтальную проекцию k₁ определяем по условию принадлежности точки к плоскости a(АВС) точка К принадлежит плос-кости a, т.к. она принадлежит прямой n₁ принадлежащей a.