К плоскости проекции

Это частный случай параллельного перемещения. Отличие в том, что траектория перемещения каждой геометрической фигуры представляет собой не произвольную линию, а дугу окружности, центр которой находится на этой оси вращения, а радиус равен расстоянию между точкой и осью вращения.

При вращении вокруг оси, перпендикулярной V, точка будет перемещаться в плоскости, перпендикулярной оси вращения, а следовательно, параллельной Н. Окружность, по которой движется точка, проецируется, таким образом, на V без искажения, а на Н в отрезок, параллельный оси х.

Пример 1. [АВ] перевести в положение, параллельное V (Рис.6.4.).

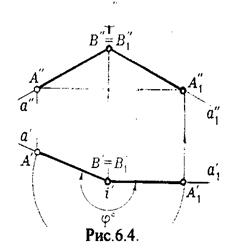Вращение производили вокруг оси i ^ H. Ось i для упрощения геометрических построений проведена через точку В, следовательно она не будет менять своего положения в процессе преобразования. Для нахождения точки А^// необходимо из А^/ провести перпендикуляр к оси х и отметить точку его пересечения с горизонтальной прямой, проведенной через a^//.

Пример 2. [CD] перевести в положение, перпендикулярное V (Рис.6.5.).

В этом случае следует осуществить два вращения вокруг осей, перпендикулярных плоскостям проекций.

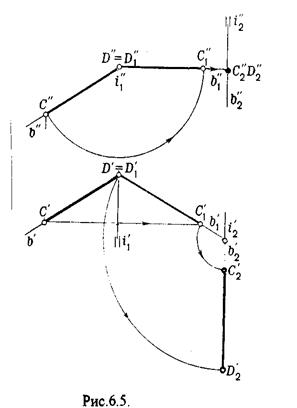В начале вращение производим вокруг i₁^V, в результате которого [АВ] занимает положение, параллельное Н, а затем переводим [АВ] в горизонтально - проецирующее положение вращением вокруг оси перпендикулярной Н.

В случае перевода плоскости общего положения в частное решается аналогично.

Чтобы плоскость общего положения заняла проецирующее положение, достаточно горизонталь или фронталь перевести в проецирующее положение. При повороте линии уровня на угол j на такой же угол повернется и все множество точек этой плоскости.

Если необходимо преобразовать плоскость в положение, параллельное плоскости проекции, необходимо осуществить еще одно вращение на какой - то угол так, чтобы вырожденная проекция плоскости (прямая, в которую проецируется плоскость) заняла положение, параллельное оси х..