АКСОНОМЕТРИЧЕСКИЕ ПРОЕКЦИИ

В переводе с греческого языка слово «аксонометрия» означает измерение по осям. Аксонометрическая проекция получается при проецировании предмета вместе с осями координат на картинную плоскость. При этом ни одна из осей системы координат не проецируется в точку. Использование аксонометрического проецирования позволяет повысить наглядность изображения фигуры.

Рассмотрим проекционную схему получения аксонометрической проекции простейшей фигуры – точки (рис. 69). Точка A и пространственная система координат Oxyz связаны координатной ломаной ОA_xA₁A, звеньями которой являются координатные отрезки [OA_x] = [x_A], [A_xA₁] = [y_A], [A₁A] = [z_A].

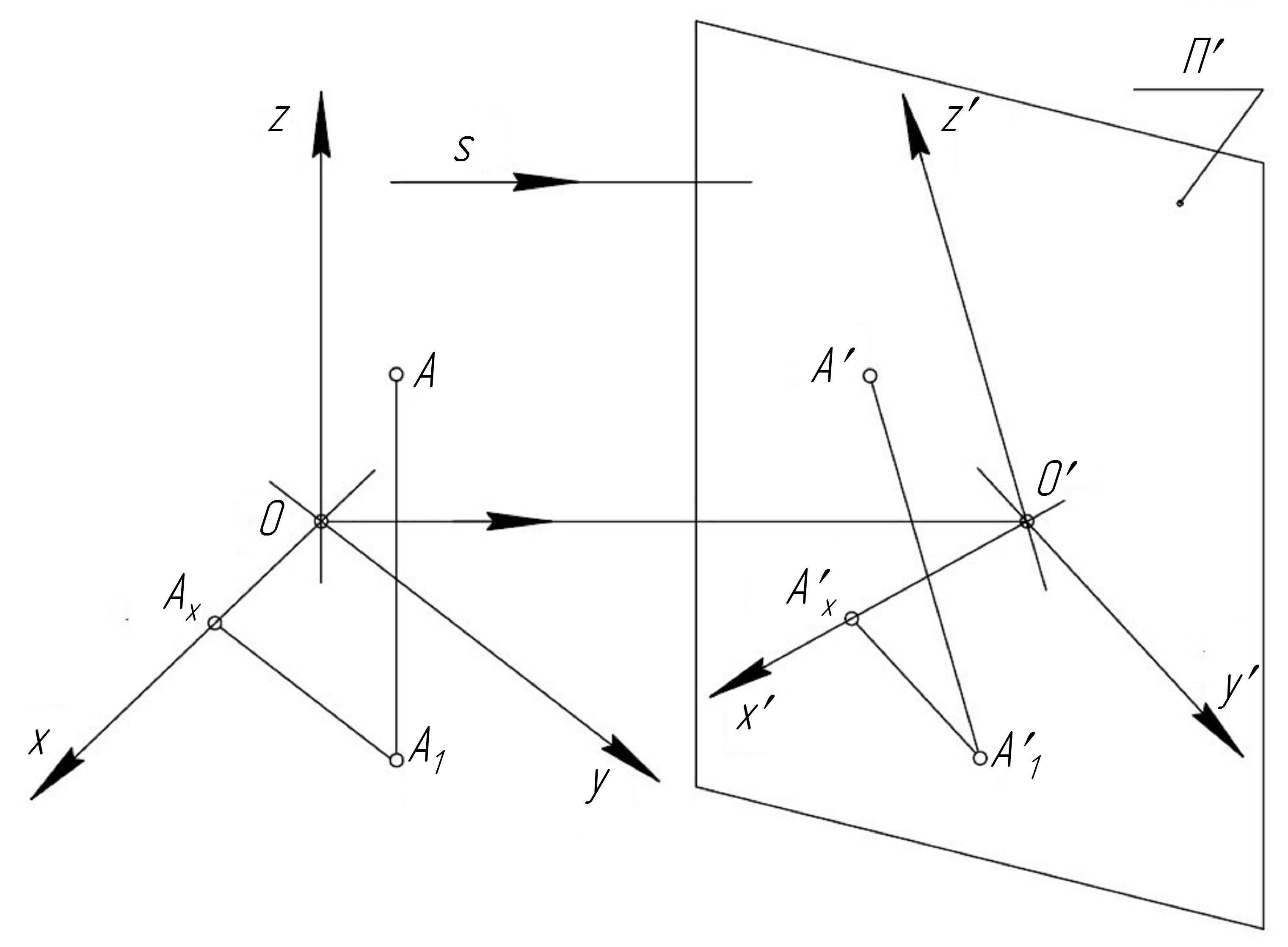
Рис. 95 Аксонометрическая проекция

Плоскость П^/ – аксонометрическая плоскость, луч s – направление проецирования. Все проецирующие прямые параллельны лучу s.

Обозначим: , , . Величины p, k, q называют коэффициентами искажения аксонометрических отрезков.

Наглядность аксонометрических проекций зависит от выбора направления проецирования. Таким образом, аксонометрические проекции делятся на прямоугольные и косоугольные.

1) Прямоугольные, если проецирующие лучи S располагаются перпендикулярно к плоскости чертежа.

2)

Кроме того, аксонометрические проекции классифицируют еще по величине коэффициентов искажения аксонометрических отрезков:

1) если все три показателя искажения (p, k, q) равны между собой, то аксонометрическую проекцию называют изометрической или сокращенно изометрией;

2) если два показателя искажения равны между собой (не равны третьему), то аксонометрическую проекцию называют диметрической или диметрией;

3) если все три показателя искажения различны, то аксонометрическую проекцию называют триметрической или триметрией.

ГОСТ 2.317-2011 устанавливает два вида прямоугольных аксонометрических проекций – изометрическую и диметрическую, и три вида косоугольных – фронтальную изометрическую, горизонтальную изометрическую и фронтальную диметрическую.