Аксонометрические проекции. Название аксонометрическая происходит от древнегреческих слов аксон – ось и метрио – измеряю
Название аксонометрическая происходит от древнегреческих слов аксон – ось и метрио – измеряю. Метод аксонометрического проецирования состоит в том, что данная фигура вместе с осями прямоугольных координат, к которым она отнесена в пространстве, проецируется на некоторую плоскость проекций, называемую аксонометрической плоскостью проекций или картинной плоскостью. В зависимости от вида проецирования аксонометрическая проекция называется:
Ø центральной – используется центральное проецирование;
Ø параллельной – используется параллельное проецирование.
Причем в последнем случае аксонометрическая проекция может быть косоугольной (при косоугольном проецировании) и ортогональной или прямоугольной (при ортогональном проецировании).
В нашем курсе мы рассмотрим лишь параллельную и ортогональную аксонометрические проекции. На рис.1.6 показана схема проецирования точки А на некоторую аксонометрическую плоскость проекций П0 по направлению проецирования S.
Рис.1.6 
Прямые ОХ, ОY, ОZ являются осями натуральной системы координатОХYZ, а прямые О0Х0, О0Y0, О0Z0 - осями аксонометрической системы координатО0Х0Y0Z0. Отрезок епринят за натуральную масштабную единицу, а отрезки ех, ey, еz - за аксонометрические масштабные единицы по соответствующим осям координат. Проекция точки А на горизонтальную плоскость ХОY обозначена А1.
Трёхзвенная пространственная линия ОАХА1А, определяющая положение точки А относительно натуральной системы координат ОХYZ, называется натуральной координатной ломаной. Звенья этой ломаной являются отрезками координат: ОАх - отрезок абсциссы, АхА1 - отрезок ординаты, А1А - отрезок аппликаты точки А. Длины отрезков координат точки А, измеренные установленной натуральной масштабной единицей е, называются натуральными координатами точки А:
; 
; 
.
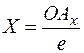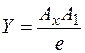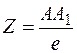Точка A0 - аксонометрическая проекция точки А. Плоская ломаная О0Ах0А10А0, которая называется аксонометрической координатной ломаной, является проекцией натуральной координатной ломаной. Так как при параллельном проецировании сохраняется простое отношение трех точек, получим:
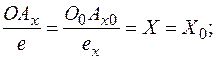
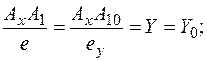
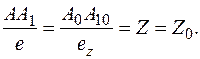
Мы получили основное свойство аксонометрических проекций: аксонометрические координаты точек, измеренные аксонометрическими масштабами, численно равны натуральным. Таким образом, особенность рассматриваемого метода аксонометрии заключается в том, что это есть координатный метод построения наглядного однокартинного чертежа, обладающего свойством обратимости.
Для удобства построения аксонометрических чертежей используют показатели искажения - отношения аксонометрического масштаба к натуральному масштабу:
; 
; 
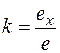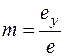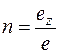. (1.1)
Если все три коэффициента искажения равны между собой, аксонометрическая проекция называется изометрической; если равны между собой любые два коэффициента искажения, проекция называется диметрической; если все коэффициенты различны - проекция называется триметрической. При построении аксонометрических проекций обычно пользуются некоторыми величинами, пропорциональными коэффициентам искажения. Эти величины называются приведенными коэффициентами искажения.
Приведем теорему Польке, которая дает ответ на вопрос, как можно выбрать на чертеже аксонометрические оси и аксонометрические масштабы. Три отрезка произвольной длины, лежащие в одной плоскости и выходящие из одной точки под произвольными углами друг к другу, представляют собой параллельную проекцию трех равных отрезков, отложенных на осях прямоугольной системы координат от ее начала.
Исходя из этой теоремы, можно взять на плоскости П0 три проходящие через одну точку несовпадающие прямые, отложить на них три произвольной длины отрезка ех, еy, еz и утверждать, что данную фигуру можно рассматривать, как параллельную проекцию прямоугольной системы координат ОХYZ с отложенными на ее осях масштабного коэффициента е. Следовательно, параллельная аксонометрическая проекция в общем случае определяется пятью независимыми параметрами: тремя аксонометрическими масштабами и двумя углами между аксонометрическими осями.
Плоскость аксонометрических проекций, пересекая плоскости натуральной системы координат, образует треугольник, называемый треугольником следов. Рассмотрим прямоугольную аксонометрию. Доказано, что в этом случае треугольник следов является остроугольным. При этом отрезок ОО0 перпендикулярен плоскости П0 (рис.1.7). Отрезки О0Х0, О()Y0, О0Z0 (аксонометрические проекции отрезков на осях координат) являются катетами прямоугольных треугольников, а сами отрезки на осях координат - гипотенузами. Отсюда:
; 
; 
.
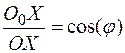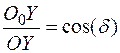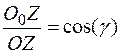Но эти отношения представляют собой коэффициенты искажения k, m, n. Следовательно, k=соs(j), m=соs(d), n=соs(g).
Справедлива следующая теорема: сумма квадратов показателей искажения в ортогональной аксонометрии равна двум:
k2+m2+n2=2. (1.2)
Из теоремы следует, что можно задаваться лишь двумя показателя искажения, а третий должен определяться по формуле (1.2). Выясним, какие значения могут принимать показатели искажения в ортогональной аксонометрии. Из формул (1.1) следует
0≤k≤1; 0≤m≤1; 0≤n≤1. (1.3)
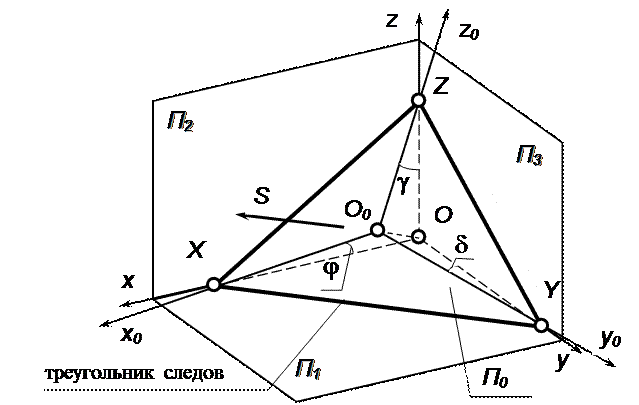
Рис.1.7
Равенство одного из показателей искажения нулю, говорит о том, что соответствующая натуральная ось координат перпендикулярна к аксонометрической плоскости проекций П0 (соs90°=0), а две другие оси координат ей параллельны. Равенство одного из показателей единице означает, что соответствующая натуральная ось координат параллельна аксонометрической плоскости проекций П0 (соs0°=1).
Не всякие три числа, удовлетворяющие условию (1.3), могут являться показателями искажения. Из (1.3) следует, что
0£k2£1; 0£m2£1; 0£n2£1. (1.4)
Если принять во внимание условие (1.2), можно написать:
1£k2+m2£2; 1£k2+n2£2; 0£n2+m2£1. (1.5)
Следовательно, в ортогональной аксонометрической проекции величины коэффициентов искажения должны быть такими, чтобы сумма квадратов любых двух показателей искажения была бы не менее единицы и не более двух. Кроме того доказано, что показатели искажения определяют направления аксонометрических осей и, наоборот, заданием аксонометрических осей определяются и показатели искажения. Таким образом, ортогональная аксонометрическая проекция определяется двумя параметрами: двумя показателями искажения или двумя углами между аксонометрическими осями
Для косоугольной аксонометрии зависимость между показателями искажения выражается следующей формулой:
k2+m2+n2=2+ctg(a), (1.6)
где a - угол наклона направления проецирования к плоскости проекций. Из этой формулы следует, что в косоугольной аксонометрии показатели искажения должны удовлетворять следующим условиям:
0£k<¥; 0£m<¥; 0£n<¥. (1.7)
Однако не всякие три числа, удовлетворяющие указанным условиям, могут являться показателями искажения в косоугольной аксонометрии. Сумма квадратов двух любых показателей искажения должна удовлетворять следующим условиям:
1£k2+m2<¥; 1£k2+n2<¥; 1£n2+m2<¥. (1.8)
Остановимся на стандартных видах аксонометрических проекциях. ГОСТ 2.317-69 рекомендует к применению на чертежах следующие пять видов аксонометрических проекций.
1. Ортогональная изометрия. Показатели искажения равны между собой ( k = m = n =0.82). На практике чаще всего используют приведенные показатели искажения, которые принимают равными 1. Поэтому изображение в этом случае увеличивается в 1.22 раза. Треугольник следов в этой проекции равносторонний, а значит углы между аксонометрическими осями координат равны 120° (рис.1.8).
2. Ортогональная диметрия. Соотношение показателей искажения принимается k = n =2m. Тогда их величина должна быть равна k = n » 0.94 , m » 0.47. Вместо этих значений пользуются приведенными показателями искажения k = n =1, m = 0.5 (изображение увеличивается в 1.06 раза). Расположение осей аксонометрической системы координат показано на рис.1.9.
3. Косоугольная фронтальная изометрия. Показатели искажения следующие: k = m = n =1. Расположение осей аксонометрической системы координат показано на рис. 1.10.
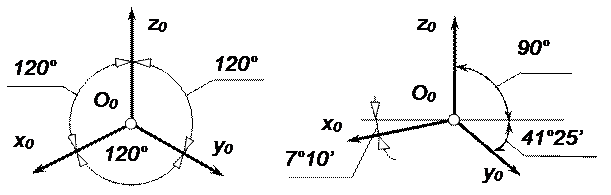
Рис.1.8 Рис.1.9
4. Косоугольная горизонтальная изометрия. Показатели искажения следующие: k = m = n =1. Расположение осей аксонометрической системы координат показано на рис.1.11.
5. Косоугольная фронтальная диметрия. Показатели искажения k = n = 1, m =0.5. Расположение осей аксонометрической системы координат показано на рис.1.12.
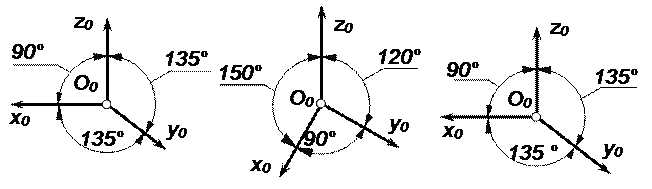
Рис.1.10 Рис.1.11 Рис.1.12
5. Развитие геометрии: Эвклид Þ Лобачевский Þ Риман
Основные закономерности и свойства пространства, составляющие содержание элементарной геометрии, излагались еще до нашей эры в трудах греческих геометров. Особенно большое значение имели работы Эвклида, жившего в III веке до нашей эры. В своих «Началах» Эвклид изложил элементарную геометрию, которая получила название эвклидова геометрия. В основу своей геометрии Эвклид положил систему постулатов, на которых строится эта наука. Постулат означает требование. Эвклид так и пишет: «Нужно потребовать:
1. Чтобы от каждой точки к каждой точке можно было провести прямую линию.
2. Чтобы ограниченную прямую можно было непрерывно продолжить по прямой.
3. Чтобы из любого центра любым радиусом можно было описать окружность.
4. Чтобы все прямые углы были друг другу равны.
5. Чтобы всякий раз, как прямая, пересекая две прямые, образует с ними внутренние односторонние углы, составляющие вместе меньше двух прямых, эти прямые при неограниченном продолжении пересекались с той стороны, с которой эти углы составляют меньше двух прямых» (рис.1.13).
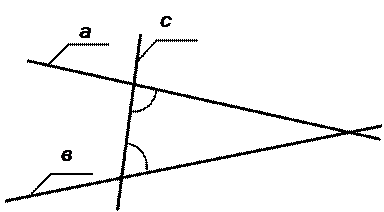
Рис.1.13
Пятый постулат, называемый как постулат о параллельных прямых, гораздо сложнее первых четырех и лишен их наглядности, потому, что речь здесь идет о неограниченном продолжении прямых. Он скорее похож на теорему, которая нуждается в доказательстве. Эвклид отводил пятому постулату особое место среди его аксиом. Изложение материала он разбил на две части. Сначала Эвклид рассматривает теоремы, которые можно доказать, не прибегая к помощи пятого постулата. Эта часть теперь называется абсолютной геометрией. Затем сгруппированы все теоремы, которые доказываются только на основе пятого постулата. Эту часть и называют собственно эвклидовой геометрией.
Многие математики последующих веков, считая пятый постулат теоремой, пытались его доказать. Однако в течении 2000 лет им этого сделать не удалось. Кроме новых формулировок[1] пятого постулата, других успехов не было. Так продолжалось до 11 февраля 1826 года, когда на заседании Ученого Совета Казанского университета профессор Николай Иванович Лобачевский (1792-1856) сообщил о создании им новой геометрии, построенной на отрицании пятого постулата Эвклида.
Свою геометрию Лобачевский назвал воображаемой или пангеометрией. В противоположность постулату Эвклида, Лобачевский в основу построения теории параллельных линий положил следующую аксиому:
Дата добавления: 2016-02-02; просмотров: 1662;