Метод перемены плоскостей проекций.

Сущность метода перемены (замены) плоскостей состоит в переходе от данной системы плоскостей проекций к новой. При этом геометрические фигуры в процессе преобразования остаются на месте, а их новые проекции получаются за счет введения дополнительных плоскостей проекций. Новые плоскости выбираются перпендикулярно старым.

При выборе положения новой плоскости проекции следует руководствоваться тем, чтобы проецируемая фигура занимала частное положение относительно новой плоскости.

Рис.6.6.

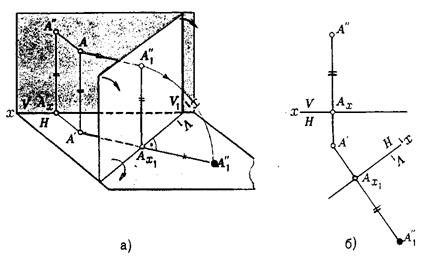Рассмотрим изменение положения точки А, если V заменить новой плоскостью V₁(V₁^ H). Горизонтальная плоскость не меняет своего положения, т.е. мы осуществляем переход от системы x(V/H) к новой x₁(V₁/H) (рис.6.6.а.). Плоскость V₁ пересекает Н по прямой х₁т.е. по новой оси.

Горизонтальная проекция А¢ не изменяет своего положения. Для нахождения новой фронтальной проекции А₁² следует провести линию связи перпендикулярно x₁ от А₁¢. Из рис.6.6. видно, что расстояние от новой фронтальной проекции А₁² до новой x₁ равно расстоянию от старой фронтальной проекции А² до старой оси х.

Совмещая V₁ с Н, перейдем от пространственной модели к эпюру. За ось вращения принимается х₁, направление поворота не влияет на результаты преобразования (рис.6.6.б.).

Иногда замена одной проекции не обеспечивает получения требуемого вида проекции, поэтому приходится переходить к замене двух плоскостей. Но одновременно меняется только одна плоскость проекции.

Пример 1.[АВ] перевести в положение, параллельно фронтальной плоскости проекций (Рис.6.7.).

Рис.6.7.

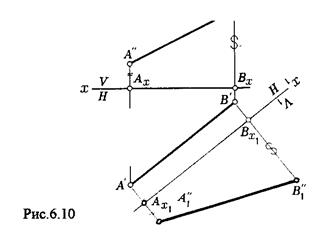
Горизонтальная проекция прямой, параллельной фронтальной плоскости проекции, всегда параллельны оси х. Отсюда следует, что новую ось x надо выбирать параллельно А'В'. Остальные геометрические построения не требуют пояснений.

Пример 2. [АВ] перевести в горизонтально- проецирующее положение (Рис.6.8.).

В этом случае следует произвести замену плоскостей дважды. Сначала меняем горизонтальную плоскость Н на новую H₁, т.е. переходим к системе x₁(V/H₁). В результате этого преобразования отрезок [АВ] займет положение, параллельное Н. Затем произведем замену старой фронтальной плоскости V на V₁, т.е. перейдем к системе x₂(V₁/H₁).

Рис.6.8.

Положение новой фронтальной проекции точки на плоскости V₁ определяется аналогично только что рассмотренному примеру. Отличие состоит лишь в том, что теперь за исходную (старую) систему будем принимать x₁(V/H₁) и от нее переходить к системе x₂(V₁/H₁). В этом случае плоскость h₁ не меняет своего положения в пространстве, следовательно не изменится положение и горизонтальной проекции A₁'B₁'. Например, фронтальная проекция А₂" будет определена, если из a₁' восставить к оси х₂ и отложить на нем расстояние, равное расстоянию от старой оси x₁ до старой фронтальной проекции А₁".

Рис.6.9.

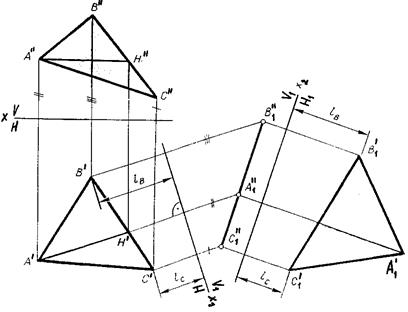Пример 3. Определить натуральную величину треугольника ABC (рис.6.9.)

Для решения такой задачи следует провести две последовательные замены плоскостей. В начале произведем замену фронтальной плоскости проекций V на V₁ т.е. перейдем к новой системе координатных плоскостей X₁(V₁/H).

Новую ось X₁ выбираем перпендикулярно к горизонтальной проекции горизонтали h¢. Плоскость треугольника ABC рассматриваем в этом случае как множество горизонталей, которые проецируются в точке, лежащие на одной прямой.

В результате этого преобразования плоскость треугольника ABC займет проецирующие положение. Чтобы перевести плоскость треугольника ABC в положение плоскости уровня (в этом случае треугольник ABC будет проецироваться в НВ), следует провести еще одну замену плоскостей, т.е. перейти к системе X₂(V₁/H₁). Ось Х₂ проходит параллельно новой проекции А₁²В₁²С₁².

Остальные геометрические построения не требуют пояснения.

<9 10 111213 14 15 >

Дата добавления: 2016-01-20; просмотров: 1006;