Пересечение прямой общего положения с плос-костью общего положения.
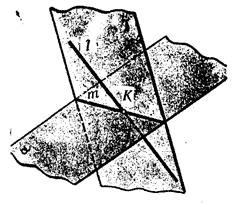
Построение точки пересе-чения произвольной прямой с плоскостью общего положения выполняют по следующему алгоритму (рис.5.11.).
1) Через данную прямую 1 проводится вспомогательная секущая плоскость (g)
2) Определяется прямая (m) пересечения заданной плоскости (a) и вспомо-гательной (g).
3) Находится точка К в пересечении прямых – данной 1 и построенной (m).
|
На рис.5.12 и 5.13. показано построение точки пересечения прямой 1 с плоскостью общего положения a, заданной треугольником ABC.
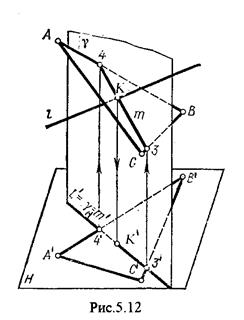
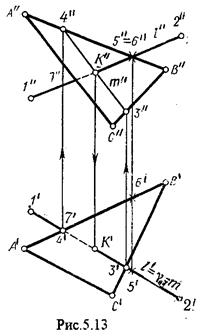
Через прямую 1 проведена вспомогательная горизонтально-проецирующая плоскость. Её горизонтальный след пересекается с А¢В¢ и А¢С¢ в точках 3¢ и 4¢, определяющих горизонтальную проекцию а линии пересечения g и a. Затем находим 3² и 4² и проводим проекцию m². В пересечении m² и 1² - определяет фронтальную проекцию К² искомой точки К. К¢ определяем по условию принадлежности К¢ Î 1.
Считая что плоскость непрозрачна определяем видимые и невидимые участки прямой 1 относительно плоскостей Н и V.
Для этого рассмотрим конкурирующие точки. Например: 5² и 6², 5Î1, 6ÎАВ.
По расположению горизонтальных проекций 5¢ и 6¢ заключаем, что участок прямой 2К находится перед плоскостью a и является на фронтальной проекции видимым. Остальная часть линии невидимая.
Аналогично, с помощью конкурирующих точек 7 и 4 определяем участки прямой на горизонтальной проекции. По расположению фронтальных проекций 7² и 4² заключаем, что участок прямой К1 расположен ниже плоскости a, следовательно, невидимый на горизонтальной проекции.
|
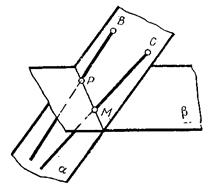 Этот алгоритм используется при определении линии пересечения двух плоскостей. Точки, принадлежащие линии пересечения определяются в пересечении прямых принадлежащих плоскости a с плоскостью b (рис.5.14).
Этот алгоритм используется при определении линии пересечения двух плоскостей. Точки, принадлежащие линии пересечения определяются в пересечении прямых принадлежащих плоскости a с плоскостью b (рис.5.14).
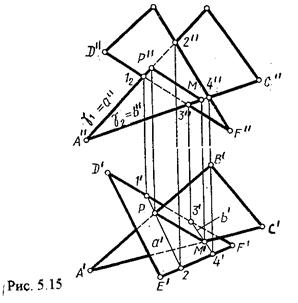
На рис. 5.15 точки Р и М. Р является пересечением АВ и АС с треугольником DEF.
Дата добавления: 2016-01-20; просмотров: 694;
