Методом прямоугольного треугольника
Отрезки прямых общего положения ни на одну из плоскостей проекций не проецируется в натуральную величину (НВ).
|
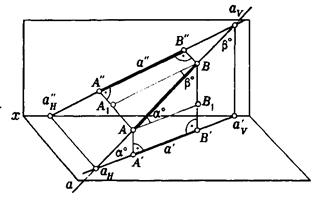Натуральная величина отрезка общего положения равна гипотенузе прямоугольного треугольника, одним катетом которого является проекция отрезка на одну из плоскостей проекций, а другим разность расстояний концов отрезка от этой же плоскости (рис.3.7.).
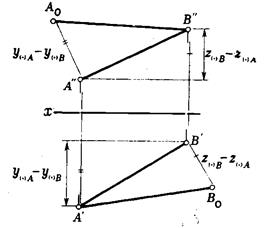
Из рисунка 3.7. видно, что угол наклона прямой к плоскости проекций определяется как угол, составленный прямой с ее проекцией на эту плоскость. Этот угол входит и в прямоугольный треугольник который строят для определения НВ отрезка (Рис.3.8.). Таким образом, угол между катетом - проекцией и гипотенузой прямоугольного треугольника равен истинной величине угла наклона отрезка к той плоскости проекций, на которой выполнены построения.
|
4. ОРТОГОНАЛЬНЫЕ ПРОЕКЦИИ ПЛОСКОСТИ
Способы задания плоскости на чертеже
На чертеже плоскость может быть задана следующими способами:
- проекциями трех точек, не принадлежащими одной прямой;
- проекциями прямой и не принадлежащей ей точки;
- проекциями пересекающихся прямых;
- проекциями параллельных прямых;
- проекциями плоской геометрической фигуры;
- следами.
Следы плоскости
Прямую, по которой плоскость пересекает плоскость проекций, называют следом плоскости (рис.4.1.).
При этом различают:
- горизонтальный след - прямая, по которой плоскость пересекает горизонтальную плоскость проекций H (aн);
- фронтальный след - прямая, по которой плоскость пересекает фронтальную плоскость проекций V(av);
| |
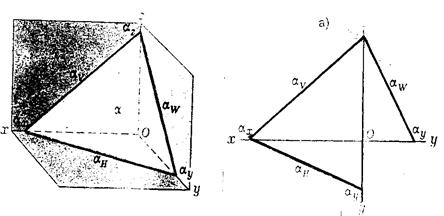- профильный след - прямая, по которой плоскость пересекает профильную плоскость проекций W(aw).
|
Для того, чтобы построить следы плоскости, надо найти следы двух произвольных прямых, принадлежащих этой плоскости.
Плоскость, не параллельную и не перпендикулярную ни к одной из плоскостей проекций, называют плоскостью общего положения.
Дата добавления: 2016-01-20; просмотров: 1057;