Плоскостная модель координатных плоскостей (эпюр)
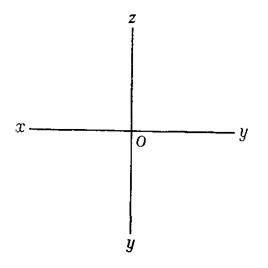 Пространственной моделью координатных плоскостей пользоваться на чертеже неудобно, поэтому ее преобразуют в эпюр, т.е. чертеж, составленный из двух или более связанных между собой проекций геометрической фигуры. Для этого горизонтальную и профильную плоскость проекции совмещают с фронтальной плоскостью проекции путем поворота плоскости Н на 90° вокруг оси х по часовой стрелке и плоскости W на 90° вокруг оси z против часовой стрелки. Отрицательное нап-равление осей на эпюре не указывается, и в окончательном виде эпюр, заменяющий пространственную модель, примет вид, показанный на рис. 1.7.
Пространственной моделью координатных плоскостей пользоваться на чертеже неудобно, поэтому ее преобразуют в эпюр, т.е. чертеж, составленный из двух или более связанных между собой проекций геометрической фигуры. Для этого горизонтальную и профильную плоскость проекции совмещают с фронтальной плоскостью проекции путем поворота плоскости Н на 90° вокруг оси х по часовой стрелке и плоскости W на 90° вокруг оси z против часовой стрелки. Отрицательное нап-равление осей на эпюре не указывается, и в окончательном виде эпюр, заменяющий пространственную модель, примет вид, показанный на рис. 1.7.
| Октанты | Знаки координат | ||
| X | У | z | |
| I | + | + | + |
| II | + | — | + |
| III | + | - | — |
| IV | + | + | — |
| V | — | + | + |
| VI | - | - | + |
| VII | _ | - | — |
| vni | - | + | - |
|
2. ОРТОГОНАЛЬНЫЕ ПРОЕКЦИИ ТОЧКИ
Положение точки в пространстве определяется координатами (х, у, z), показывающими величины расстояний, на которые точка удалена от плоскостей проекций (рис.2.1.)
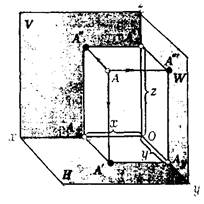
Рис.2.1.
Чтобы определить эти расстояния, достаточно через точку А провести прямые, перпендикулярные к плоскостям проекций, определить точки А', А", А'" встречи этих прямых с плоскостями проекций и измерить величины отрезков [АА'], [АА"3, [АА'"], которые укажут соответственно значения аппликаты z, ординаты у и абсциссы х точки А.
Точки А', А", А'" называют ортогональными проекциями точки А, при этом согласно принятым обозначениям:
А' - горизонтальная проекция точки А;
А" - фронтальная проекция точки А;
А'" - профильная проекция точки А.
Прямые (АА'), (АА"), (АА'") называют проецирующими прямыми или прое-цирующими лучами.
Эпюр точки А, представленный на рис.2.2., несет ту же информацию, что и пространственный макет. Горизонтальная проекция точки А определяется координатами х, у т.е. расстоянием от точки А до плоскостей W и V.
А'(х, у).
Фронтальная проекция точки А определяется координатами х и z, т.е. расстоянием от A floW и Н.
А"(х, z).
Профильная проекция точки А определяется координатами у и z, т.е. расстоянием от V и Н.
А'"(у, z).
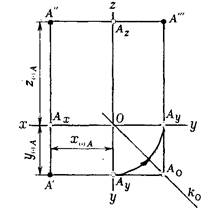 Анализируя рис.2.2., можно сделать следующие выводы: фронтальная и профильная проекции точки всегда находятся на одной горизонтальной линии связи; фронтальная и горизонтальная проекции точки всегда находятся на одной вертикальной линии связи. Таким образом, можно построить недостающую третью проекцию.
Анализируя рис.2.2., можно сделать следующие выводы: фронтальная и профильная проекции точки всегда находятся на одной горизонтальной линии связи; фронтальная и горизонтальная проекции точки всегда находятся на одной вертикальной линии связи. Таким образом, можно построить недостающую третью проекцию.
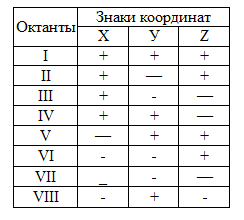 Рис.2.2.
Рис.2.2.
Положение точки в пространстве можно определить, если будут заданы хотя бы две ее координаты. Зная направление для положи-тельного и отрицательного значений координатных осей, определяется принадлеж-ность точки какому -либо из восьми октантов. Для этого можно составить следующую таблицу:
Дата добавления: 2016-01-20; просмотров: 1301;
