ОРТОГОНАЛЬНЫЕ ПРОЕКЦИИ ПРЯМОЙ

Прямая линия определяется двумя точками, чтобы построить эпюр прямой, надо построить проекции лишь двух ее точек.

Прямая в пространстве может быть расположена относительно плоскостей проекций по-разному. Прямую, не параллельную и не перпендикулярную ни к одной из плоскостей проекций, называют прямой общего положения.

Следы прямой

Прямая общего положения пересекает все три плоскости проекций.

Точку пересечения (встречи) прямой с плоскостью проекции называют следом прямой. Точка пересечения прямой 1 с горизонтальной плоскостью проекций называется горизонтальным следом прямой l_h, с фронтальной - фронтальным следом прямой l_v, с профильной - профильным следом прямой l_w (рис.3.1.).

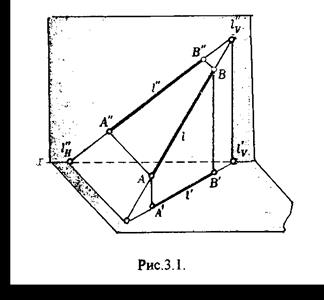
l_H¢, 1_H", 1_H¢¢¢, lv', lv", lv'", l_W', lw", lw'" - соответственно горизонтальная, фронтальная, профильная проекции следов 1_H, lv , lw. Очевидно, что 1_Н'= 1_H", lv"= lv , lw'"= l_W.

Чтобы построить на чертеже горизонтальный след прямой 1 (рис.3.2.), надо продолжить фронтальную проекцию прямой 1 до пересечения с осью х в точке 1н", затем, используя принцип принадлежности точки прямой достроить 1_Н'.

Для построения фронтального следа прямой 1 надо продлить горизонтальную проекцию прямой 1 до пересечения с осью х в точке lv' и достроить по соответствующим линиям связи l_V".

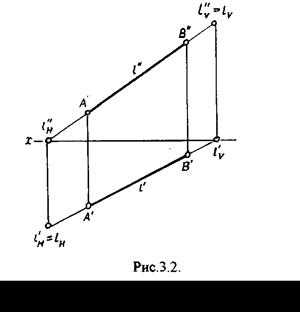
Аналогично строится профильный след прямой 1. Для этого продолжают либо фронтальную проекцию прямой I до пересечения с осью z в точке l_W", либо горизонтальную проекцию 1 до пересечения с осью у в точке l_W' и по соответствующим линиям связи достраивают недостающие проекции.