Прямая как линия пересечения плоскостей
Прямая в пространстве может быть определена как линия пересечения двух непараллельных плоскостей 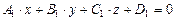 и
и 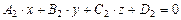 , то есть как множество точек, удовлетворяющих системе двух линейных уравнений
, то есть как множество точек, удовлетворяющих системе двух линейных уравнений
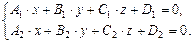 (V.5)
(V.5)
Справедливо и обратное утверждение: система двух независимых линейных уравнений вида (V.5) определяет прямую как линию пересечения плоскостей (если они не параллельны). Уравнения системы (V.5) называются общим уравнением прямой в пространстве 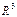 .
.
Пример V.12.Составить каноническое уравнение прямой, заданной общими уравнениями плоскостей
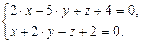
Решение.Чтобы написать каноническое уравнение прямой или, что тоже самое, уравнение прямой, проходящей через две данные точки, нужно найти координаты каких-либо двух точек прямой. Ими могут служить точки пересечения прямой с какими-нибудь двумя координатными плоскостями, например Oyz и Oxz.
Точка пересечения прямой с плоскостью Oyz имеет абсциссу 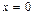 . Поэтому, полагая в данной системе уравнений
. Поэтому, полагая в данной системе уравнений 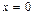 , получим систему с двумя переменными:
, получим систему с двумя переменными:
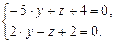
Ее решение 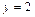 ,
,  вместе с
вместе с 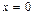 определяет точку
определяет точку 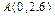 искомой прямой. Полагая в данной системе уравнений
искомой прямой. Полагая в данной системе уравнений 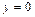 , получим систему
, получим систему
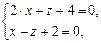
решение которой 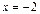 ,
, 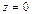 вместе с
вместе с 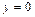 определяет точку
определяет точку 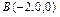 пересечения прямой с плоскостью Oxz.
пересечения прямой с плоскостью Oxz.
Теперь запишем уравнения прямой, проходящей через точки 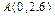 и
и 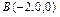 :
: 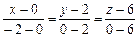 или
или 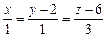 , где
, где 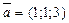 будет направляющим векто-ром этой прямой.
будет направляющим векто-ром этой прямой.
Пример V.13.Прямая задана каноническим уравнением 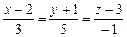 . Составить общее уравнение этой прямой.
. Составить общее уравнение этой прямой.
Решение.Каноническое уравнение прямой можно записать в виде системы двух независимых уравнений:
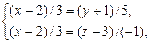 Û
Û 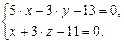
Получили общее уравнение прямой, которая теперь задана пересечением двух плоскостей, одна из которых 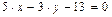 параллельна оси Oz (
параллельна оси Oz ( 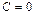 ), а другая
), а другая 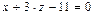 – оси Оу (
– оси Оу ( 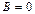 ).
).
Данную прямую можно представить в виде линии пересечения двух других плоскостей, записав ее каноническое уравнение в виде другой пары независимых уравнений:
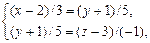 Û
Û 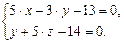
Замечание. Одна и та же прямая может быть задана различными системами двух линейных уравнений (то есть пересечением различных плоскостей, так как через одну прямую можно провести бесчисленное множество плоскостей), а также различными каноническими уравнениями (в зависимости от выбора точки на прямой и ее направляющего вектора).
Ненулевой вектор, параллельный прямой линии, будем называть ее направляющим вектором.
Пусть в трехмерном пространстве  задана прямая l, проходящая через точку
задана прямая l, проходящая через точку 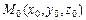 , и ее направляющий вектор
, и ее направляющий вектор 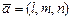 .
.
Любой вектор  , где
, где 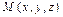 , лежащий на прямой, коллинеарен с вектором
, лежащий на прямой, коллинеарен с вектором  , поэтому их координаты пропорциональны, то есть
, поэтому их координаты пропорциональны, то есть
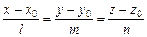 . (V.6)
. (V.6)
Это уравнение называется каноническим уравнением прямой. В частном случае, когда ﻉ есть плоскость, получаем уравнение прямой на плоскости
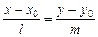 . (V.7)
. (V.7)
Пример V.14. Найти уравнение прямой, проходящей через две точки 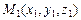 ,
, 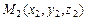 .
.
Будем считать вектор 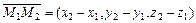 направляющим, тогда уравнение искомой прямой имеет вид
направляющим, тогда уравнение искомой прямой имеет вид
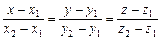 ,
,
где 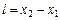 ,
, 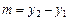 ,
, 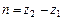 .
.
Удобно уравнение (V.6) записать в параметрической форме. Так как координаты направляющих векторов параллельных прямых пропорциональны, то, полагая
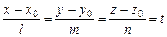 ,
,
получим
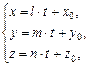
где t – параметр, 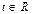 .
.
Дата добавления: 2016-01-26; просмотров: 1767;
