Расстояние от точки до прямой

Рассмотри двухмерное евклидовое пространство ﻉ
с декартовой системой координат. Пусть точка 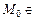ﻉ
и lÌﻉ. Найдем расстояние от этой точки до прямой. Положим 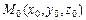,и прямая l задается уравнением 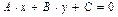(рис. V.8).

Расстояние 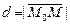, вектор 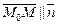, где 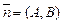– нормальный вектор прямой l, 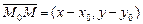и 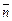– коллинеарны, поэтому их координаты пропорциональны, то есть 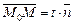, следовательно, , .

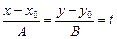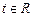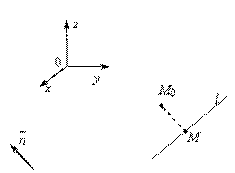
Рис. V.8

Отсюда 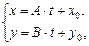или умножая эти уравнения
на A и B соответственно и складывая их, находим 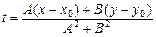, отсюда

или

.

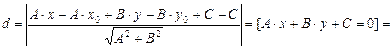
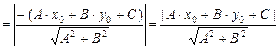Формула

(V.8)

определяет расстояние от точки 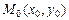до прямой .

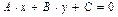Пример V.15. Найти уравнение прямой, проходящей через точку 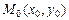перпендикулярно прямой l: 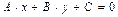и найти расстояние от 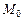до прямой l.

Из рис. V.8 имеем 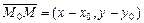, а нормальный вектор прямой l 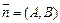. Из условия перпендикулярности имеем

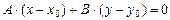
или

.

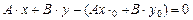Так как 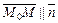, то

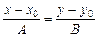. (V.9)

Это и есть уравнение прямой, проходящей через точку 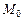, перпендикулярно прямой .

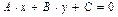Пусть имеем уравнение прямой (V.9), проходящей через точку 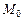, перпендикулярна прямой l: 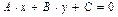. Найдем расстояние от точки 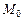до прямой l, используя формулу (V.8).

Для нахождения искомого расстояния достаточно найти уравнение прямой, проходящей через две точки 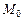и точку 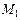, лежащую на прямой в основании перпендикуляра. Пусть 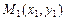, тогда

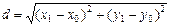. (V.10)

Так как 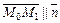, а вектор 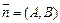, то

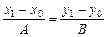. (V.11)

Поскольку точка 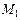лежит на прямой l, то имеем еще одно равенство 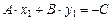или

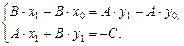
Приведем систему к виду, удобному для применения метода Крамера

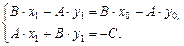
Ее решение имеет вид

,

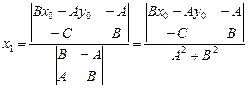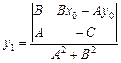. (V.12)

Подставляя (V.12) в (V.10), получаем исходное расстояние.

Пример V.16. В двухмерном пространстве задана точка 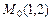и прямая 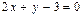. Найти расстояние от точки 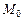до прямой; записать уравнение прямой, проходящей через точку 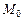перпендикулярно заданной прямой и найти расстояние от точки 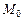до основания перпендикуляра к исходной прямой.

По формуле (V.8) имеем

.

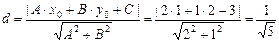Уравнение прямой, содержащей перпендикуляр, найдем как прямую, проходящую через две точк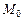и и 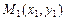, воспользовавшись формулой (V.11). Так как 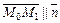, то, с учетом того, что 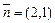, а 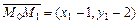, имеем

.

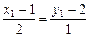Для нахождения координат 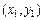имеем систему с учетом того, что точка 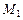лежит на исходной прямой

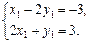
Следовательно, 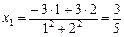, , 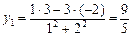отсюда .

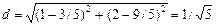Рассмотрим трехмерное евклидовое пространство ﻉ. Пусть точка 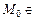ﻉ и плоскость PÌﻉ. Найдем расстояние от этой точки 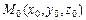до плоскости P, заданной уравнением 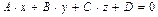(рис. V.9).

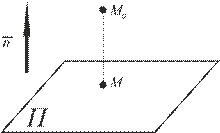
Рис. V.9

Аналогично двухмерному пространству имеем 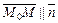и вектор 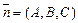, а 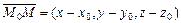, отсюда

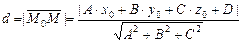. (V.13)

Уравнение прямой, содержащей перпендикуляр к плоскости P, запишем как уравнение прямой, проходящей через две точк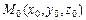и и 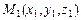, лежащую в плоскости P:

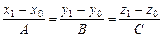. (V.14)

Для нахождения координат точки 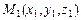к двум любым равенствам формулы (V.14) добавим уравнение

. (V.15)

Решая систему трех уравнений (V.14), (V.15), найдем 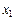, , 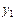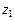– координаты точки 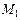. Тогда уравнение перпендикуляра запишется в виде

.

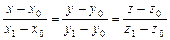Для нахождения расстояния от точки 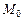до плоскости P вместо формулой (V.13) воспользуемся

.