Абсолютна швидкість точки дорівнює геометричній сумі переносної і відносної швидкостей.

З рис.26.2 маємо:

,

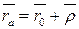але оскільки:

,

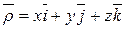то:

.

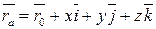(26.1)

В рухомій системі відліку 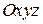з часом змінюються як координати 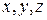точки М, так і (за напрямом) одиничні вектори 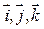цієї системи.

Тому швидкість абсолютного руху точки:

.

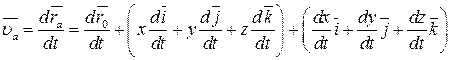(26.2)

Перший доданок у правій частині рівності (2.49) являє собою швидкість точки О відносно нерухомої системи відліку. Другий доданок– це похідна за часом від 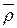в припущенні, що координати 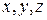точки М сталі. Тобто другий доданок – це швидкість відносно центра О тієї точки рухомої системи, яка в даний момент часу збігається з точкою М.

З цього виходить, що сума двох перших доданків правої частини рівняння (26.2) визначає швидкість відносно нерухомих координатних осей точки рухомої системи 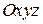, з якою в даний момент часу збігається точка М, тобто швидкість 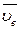переносного руху.

Третій доданок правої частини рівняння – похідна від 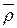в припущенні, що 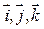сталі величини, - визначає швидкість точки М по відношенню до рухомих координатних осей, тобто і є швидкістю її у відносному русі: .

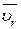З урахуванням вище викладеного рівняння (26.1) набуває вигляду:

,

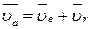(26.3)

що і потрібно було довести.

Величину абсолютної швидкості можна знайти за формулою, що визначає довжину діагоналі паралелограма швидкостей (рис.26.3):

.

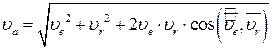(26.4)

Другим способом визначення модуля абсолютної швидкості є спосіб проекцій.

В декартовій системі координат 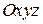векторне рівняння (26.3) відповідає трьом алгебраїчним рівнянням:

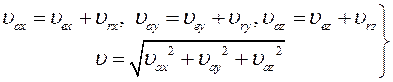
(26.5)

Іноді треба знайти відносну швидкість точки, коли відомі її переносна та абсолютна швидкості, або навпаки, треба знайти переносну швидкість, коли відомі її відносна та абсолютна швидкості.

Рис.26.3

З формули (26.3) маємо:

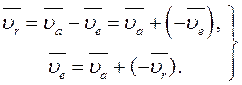
(26.6)

Величина відносної швидкості може бути визначена за формулою (рис.26.4):

.

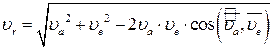(26.7)

Рис.26.4

За аналогічною формулою можна визначити і переносну швидкість. Цей спосіб називають «способом зупинки руху».