Частинні випадки знаходження МЦП

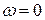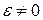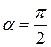1. ; . Тоді і . Цей випадок відповідає миттєво-поступальному руху. Прискорення всіх точок плоскої фігури перпендикулярні до прямих, що з’єднують ці точки з МЦП (рис.24.9).

Рис.24.9

2. 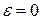, 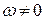. Така умова відповідає або обертанню плоскої фігури з постійною кутовою швидкістю, або випадку, коли кутова швидкість досягає екстремальних значень. Маємо: 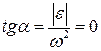і 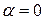. Отож, прискорення всіх точок фігури напрямлені до МЦП (рис.24.10).

Рис. 24.10

3. 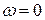; 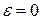. Умова відповідає поступальному руху, і прискорення будь-якої точки плоскої фігури дорівнює прискоренню полюса, а МЦП знаходиться у нескінченності.

На закінчення розділу потрібно підкреслити, що МЦШ і МЦП – це різні точки тіла (фігури). Вони збігаються лише у випадку обертання тіла навколо нерухомої осі.

Розглянемо такий приклад.

Циліндр радіуса 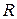котиться без ковзання по горизонтальній площині, причому швидкість його центра мас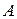 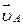є змінною. Визначити прискорення точки 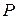контакту циліндра з площиною (рис.24.11).

Розв’язання:

Рис. 24.11

В даному випадку точка Р є миттєвим центром швидкостей котка і .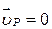

Визначимо кутову швидкість і кутове прискорення циліндра:

;

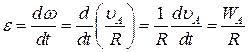
(а)

Припустимо, що циліндр котиться прискорено, тобто 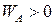. Приймаємо точку 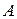за полюс, тоді прискорення точки Р визначається формулою:

.

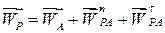(б)

Величина тангенціальної складової відносного прискорення 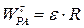і, таким чином, дорівнює величині . В той же час, як видно з рисунка, 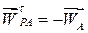. З урахуванням цього рівняння (б) набуває вигляду: .

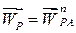Оскільки 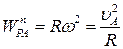, то величина прискорення точки :

.

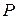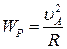Питання для самоконтролю

2.Прискорення якої точки тіла, що здійснює плоский рух, можна обчислити за рівняннями його руху?

3.За якою формулою можна визначити прискорення будь-якої точки тіла в плоскопаралельному русі? Поясніть фізичне значення окремих складових, що входять до цієї формули.

4.Чому проекція прискорення довільної точки плоскої фігури на вісь, що проходить через полюс і цю точку, не може бути більшою проекції прискорення полюса на ту ж вісь?

5.Як напрямлено прискорення точки В плоскої фігури, якщо її кутова швидкість стала, а прискорення полюса А напрямлено вздовж прямої АВ?

6.Яку точку плоскої фігури називають миттєвим центром прискорень (МЦП) і чи може МЦП співпвдвти з МЦШ?

7.Визначити напрям прискорення точки В, якщо плоска фігура здійснює миттєво-поступальний рух, а прискорення точки А перпендикулярно до прямої АВ.

8.Як напрямлено і чому дорівнює прискорення точки В плоскої фігури, якщо кутова швидкість є сталою, прискорення точки А 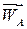перпендикулярне до відрізка АВ, а прискорення 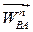за модулем рівне прискоренню ?

9.Знайдіть величину і напрям прискорення точки В плоскої фігури, якщо прискорення точки А відоме і перпендикулярне до відрізка АВ, при таких умовах:

10. а) , ;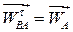

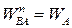11. б) , .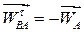

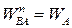12. Що можна сказати про кутову швидкість плоскої фігури, якщо прискорення точки А дорівнює нулю, а прискоренння точки В напрямлене вздовж прямої АВ?

13. Що являє собою картина розподілу прискорень точок плоскої фігури в даний момент часу по відношенню до МЦП в таких випадках:

14. а)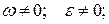

15. б)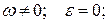

16. в)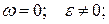

17. г)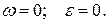

Заняття 26

План

1. Переносний, відносний та абсолютний рух точки.

2. Теорема про складання швидкостей.

ЛІТЕРАТУРА ОСНОВНА

ЛІТЕРАТУРА ДОДАТКОВА

Студенти повинні знати: визнчення переносної, відносної та абсолютної швидкостей та прискорень при складному русі матеріальної точки.

Студенти повинні вміти: визначати вид руху,а також швидкості та прискорення в будь який момент часу для точки при складному русі.