Прискорення точок при плоскопаралельному русі твердого тіла

Теорема: прискорення будь-якої точки твердого тіла, що здійснює плоский рух, дорівнює геометричній сумі прискорення полюса і прискорення даної точки в її обертальному русі навколо полюса.

Згідно з формулою (24.2) швидкість довільної точки В тіла (дивись рис.24.1).

.

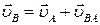Диференціюємо це рівняння за часом і отримуємо

.

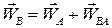(25.1)

що і потрібно було довести.

В свою чергу, прискорення 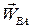, як прискорення точки в обертальному русі навколо полюса А, складається з нормального і тангенціального прискорень:

.

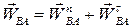(25.2)

Тоді формулі (2.41) можна надати вигляду

.

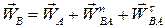(25.3)

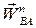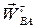Модулі векторів і визначають згідно з формулами:

,

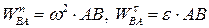причому вектор 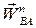напрямлений від точки В до полюса А, а вектор 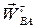перпендикулярний до відрізка АВ, що з’єднує дану точку з полюсом, і має напрям в бік напряму стрілки кутового прискорення 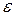(рис. 25.1).

При розв’язанні задач кінематики плоскопаралельного руху доцільно векторне рівняння (25.3) замінити алгебраїчними рівняннями його проекцій на дві обрані координатні осі. Так, наприклад, в плоскій системі координат Оху будемо мати:

.

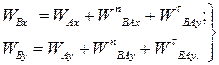(25.4)

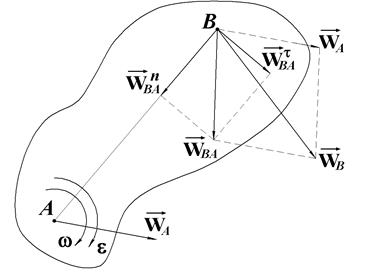
Рис.25.1