Визначення швидкості і прискорення при природному способі задання руху точки

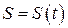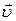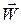При природному способі задання руху, коли відомі траєкторія точки і закон руху її вздовж цієї траєкторії , значення векторів і визначають по їх проекціях не на осі будь-якої нерухомої системи відліку, а на осі рухомої прямокутної системи координат 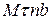.Ця координатна система має початок в точці М і рухається разом з нею вздовж траєкторії (рис.21.4).

Осі координат системи, які називають осями природного тригранника, напрямлені так: вісь 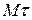(дотична) – по дотичній до траєкторії в бік додатного відліку відстані 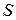; вісь (головна нормаль) – по нормалі до траєкторії в так званій стичній площині[1] в бік угнутості траєкторії; вісь 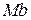(бінормаль) – перпендикулярно двом першим осям так, щоб вона утворювала з ними праву систему осей.

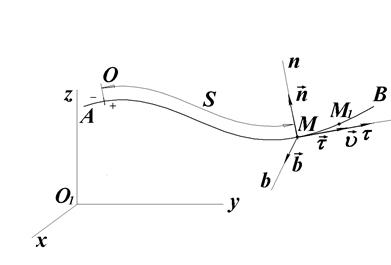
Рис.21.4

Уведемо одиничні орти 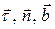, які визначають додатні напрями осей 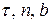натурального тригранника. Тоді вектор швидкості 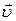точки М, що напрямлений по дотичній до траєкторії, можна подати у вигляді

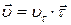(21.13)

де 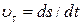– проекція вектора 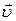на дотичну 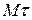– величина алгебраїчна.

Очевидно, що 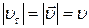, тому надалі в більшості випадків будемо опускати індекс " 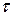" при визначенні числового значення швидкості точки.

Продиференціюємо (21.13) за часом

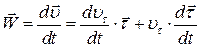(21.14)

Далі перетворимо останній член цього виразу

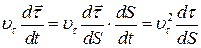(21.15)

Визначимо приріст вектора 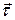на ділянці 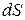переміщення точки по траекторії з положення 1 в положення 2 (рис.21.5).

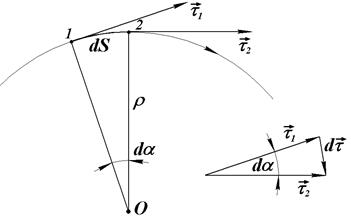
Рис. 21.5

При прагненні точки 2 до точки 1 відрізок траєкторії 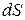наближається до дуги кола з центром в певній точці О. Цю точку називають центром кривизни траєкторії в даній точці 1, а радіус 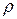відповідного кола – радіусом кривизни траєкторіїв тій же точці.

Як видно з рис 21.5, центральний кут , бо .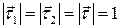

Тоді .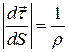

В свою чергу легко довести математично (і це можна бачити також з рис.2.5), що при 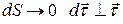, тобто вектор 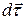співпадає з напрямом головної нормалі п. Тому, користуючись ортом головної нормалі 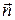, останнє співвідношення у векторній формі можна записати так:

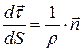(21.16)

Підставляємо (21.16) до (21.15), а отриманий вираз до (21.14). В результаті знаходимо:

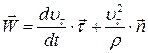(21.17)

Перший доданок цього рівняння називають тангенціальним (дотичним) прискоренням 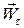, а другий – нормальним або доцентровим прискоренням :

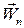(21.18)

Так як орти 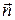і 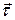лежать в стичній площині, то і вектор 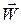також буде лежати в цій площині. Тому проекція повного прискорення на бінормаль .

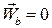Таким чином, повне прискорення точки в загальному випадку криволінійного руху

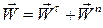(21.19)

Потрібно чітко уявляти особливості кожної складової повного прискорення. Вектор тангенціального прискорення 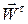напрямлений по дотичній до траєкторії точки і характеризує зміну модуля швидкості точки. Величина 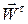може бути додатною, від’ємною або рівною нулю. Вектор нормального прискорення 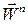завжди напрямлений в бік угнутості траєкторії і характеризує зміну вектора швидкості точки за напрямом. Величина 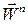завжди додатна (рис. 21.6)


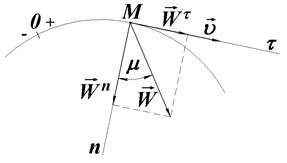
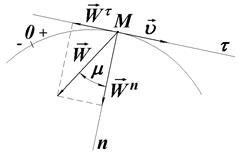
а) прискорений рух	б) сповільнений рух
Рис. 21.6

Модуль повного прискорення точки визначають за формулою

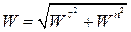(21.20)

Кут 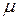відхилення вектора 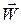від нормалі знаходять зі співвідношення

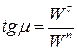
(21.21)

причому .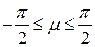

Частинні випадки руху точки.

1. 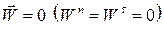– прямолінійний рівномірний рух.

2. 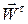=const, 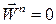– прямолінійний рівнозмінний рух.

3. 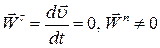– рівномірний рух точки вздовж криволінійної траєкторії будь-якої форми, або момент екстремального значення швидкості.

4. 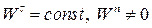– рівнозмінний криволінійний рух.

5. 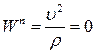– прямолінійний рух точки; момент часу, коли рухома точка знаходиться в точці перегину траєкторії, або моменти часу зміни напряму руху точки вздовж траєкторії.

Питання для самоконтролю:

1. вноприскореним, рівносповільненим?

2. Що означає в загальному випадку наявність чи відсутність нормального прискорення точки?

3. Траєкторією точки є еліпс. В яких положеннях на траєкторії точка має найбільше і найменше прискорення, якщо вона рухається рівномірно?

4. Дві точки починають рух зі стану спокою з однаковими дотичними прискореннями. Перша рухається по колу радіуса 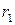, а друга – по колу радіуса , причому 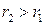. Яка точка в кожний момент часу має більше прискорення?