Введення плоскої системи сил до заданої точки
Розв’яжемо задачу про зведення довільної плоскої системи сил до заданої точки /центра/, тобто про заміну даної системи сил іншою, яка їй еквівалентна, але значно простіша і складається, як ми побачимо далі, тільки з однієї сили й пари. Для цього необхідно довести таку теорему:
Основна теорема статики :будь-яка плоска система сил, що діє на тіло, еквівалентна одній силі - головному вектору і одній парі, момент якої дорівнює головному моменту.
Нехай на тіло діє система сил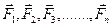 
/рис. 8.2/, розташованих у площині як завгодно, тобто вони не паралельні одна одній і лінії їх дії не перетинаються в одній точці.
Виберемо яку-небудь точку О за центр зведення і, користуючись теоремою про паралельний перенос сили, перенесемо всі сили в центр O, приєднуючи при цьому відповідні пари /див. рис. 8.2/. Тоді на тіло діятиме система сил
…………., 
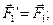
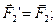
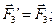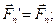
які прикладені у точці О, і система пар, моменти яких дорівнюють
; 
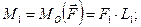
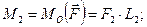
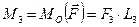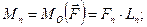
Систему збіжних сил замінюють однією силою – рівнодіючою, яку називають головним вектором.
Головний вектор дорівнює .геометричній сумі векторів усіх сил /рис. 8.3, б,в/, тобто
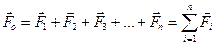/8.1/
Систему пар сил замінюють однією рівнодіючою парою сил, момент якої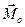 
, називають головним моментом.
Головний момент дорівнює геометричній сумі векторів моментів усіх сил відносно центра зведення, тобто
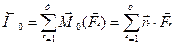/8.2/
Таким чином, ми довели, що плоска система довільно розташованих сил еквівалентна одній силі /головному вектору/ і одній парі, момент якої дорівнює головному моменту /рис. 8.3 г/.
Рис. 8.2
Головний вектор і головний момент для плоскої системи сил завжди напрямлені перпендикулярно один до одного. Це пояснюється тим, що головний вектор лежить у площині дії сил, а головний момент напрямлений перпендикулярно до пари сил, яка розташована у цій самій площині
Модуль і напрям головного вектора не залежать від вибору центра зведення /від положення точки О силовий многокутник, зображений на рис. 4.5,в, не зміниться/. Значення ж головного моменту 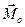залежить від вибору центра зведення /при зміні положення точки О змінюються значення моментів, сил відносно цього центра, оскільки змінюється довжина плечей 
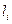/див. рис. 8.3/ і напрям моментів приєднаних пар/.
На практиці для визначення головного вектора і головного моменту користуються аналітичним методом /методом проекцій/, при цьому зручно початок прямокутної системи координат розмістити в центрі зведення /див. рис. 8.4,в/. Тоді модуль головного вектора
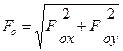; /8.3/
де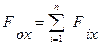 
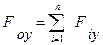проекції головного
вектора відповідно на осі X і Y.
Напрям головного вектора визначають напрямними косинусами
; 
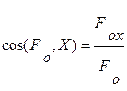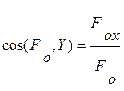/8.4/
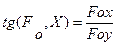. /8.5/
Враховуючи /8.1/ і /8.2/, знаходять модуль головного моменту:
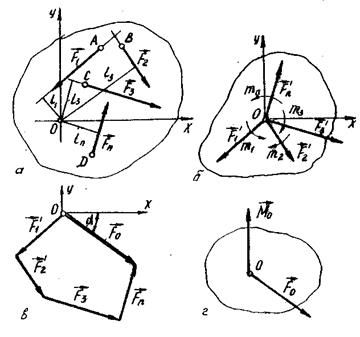
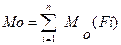. /8.6/
|
|
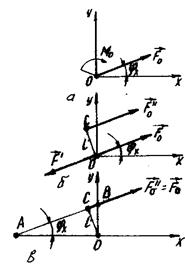
Рис. 8.3 Рис. 8.4
Дата добавления: 2016-01-26; просмотров: 2356;