Приведення сили до завданого центру ( теорема Пуансо).

Як відомо, рівнодіючу системи збіжних сил знаходять з допомогою правила паралелограма або многокутника сил. Очевидно, що аналогічну задачу можна буде розв'язати і для системи довільних сил, якщо знайти для них метод, який дозволив би перенести всі сили, що діють на тіло, в одну точку. Такий метод дає теорема про паралельний перенос си­ли в будь-яку точку /вперше довів на початку XIX ст. Л.Пуансо/.

Теорема. Будь-яку силу, що прикладена до абсолютно твердого тіла, можна, не змінюючи її дії на тіло, перенести з даної точки в ін­шу точку тіла, приєднавши пару сил, момент якої дорівнює моменту да­ної сили відносно нової точки її прикладання.

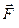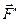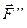Доведення. Нехай на тверде тіло діє сила , що прикладена в точці A /рис. 8.1/. Дія цієї сили не зміниться, якщо в будь-якій точці тіла О прикласти дві зрівноважені сили і такі, що .

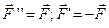Одержана система трьох сил є еквівалентна пере­носу у точку О си­ли 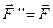і додатко­вої пари 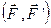момент якої відносно точки О 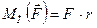/рис. 8.1/.

Iз сказаного випливає, що силу можна перенести паралельно самій собі в будь-яку точку, приєднавши при цьому пару сил, момент якої дорівнює моменту заданої сили відносно нової точки.

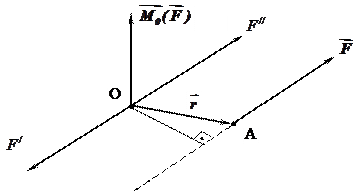Рис. 8.1

Перенос сили в іншу точку називають зведенням сили до точки; точку, в яку переносять силу, - центром зведення, додатковий момент пари, який з’явився при цьому, - моментом приєднаної пари.