Рівняння рівноваги плоскої системи довільно розташованих сил

При розв'язанні задач статики широко використовують аналітичні методи, які вимагають складання рівнянь рівноваги, умови рівнова­ги /8.7/ можна виразити трьома формами рівнянь рівноваги.

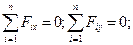Перша /основна/ форма рівнянь. Із формул /8.3/ і /8.6/ для визначення головного вектора і головного моменту плоскої системи сил випливає, що вони дорівнюватимуть нулю, якщо

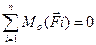/8.8/
тобто для рівноваги плоскої системи сил необхідно і достатньо, щоб сума проекцій усіх сил на кожну з двох координатних осей і алгебраїч­на сума їх моментів відносно будь-якого центра, що лежить у площині дії сил, дорівнювали нулю.

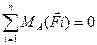Другу форму рівнянь рівноваги одержимо, якщо в системі /8.8/ замість одного рівняння моментів складемо два рівняння моментів від­носно будь-яких двох центрів, до яких додамо одне рівняння проекцій усіх званих сил на вісь, не перпендикулярних до прямої, що з’єднує ці центри, тобто

/8.9/

де вісь X не перпендикулярна лінії АВ /рис. 8.5/.

Через те що система сил знаходиться в рівновазі, згідно з /8.7/ головний момент цієї системи відносно будь-якої точки площини дорів­нює нулю, зокрема відносно точок А і В. Для рівноваги плоскої сис­теми сил одного рівняння моментів не достатньо, оскільки головний вектор може проходити, наприклад, через точку В, тоді момент від­носно точки В дорівнює нулю, а відносно точки А - не дорівнює нулю. 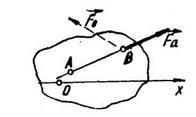Рис. 8.5

Система сил, яка задовольняє перші два рівнян­ня /4.16/, може бути неврівноважена лише тоді, коли лінія дії 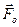збі­гається з лінією АВ як це показано на рис. 8.5. Третє рівняння /8.7/ визначає рівність нулю головного вектора.

Таким чином, для рівноваги плос­кої системи сил необхідно і достатньо, щоб алгебраїчні суми моментів усіх сил відносно будь-яких двох точок, в також сума проекцій сил на вісь, не перпендикулярну прямій, що з’єднує ці точки, дорівнювали нулю.

Третю форму рівнянь рівноваги одержимо, якщо складемо три рів­няння моментів сил відносно трьох точок, що не лежать на одній прямій:

/8.10/

Як видно з рис. 8.5, плоска система сил не буде зрівноважена тоді, коли головний вектор 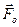проходитиме через точки А і В оскільки сума моментів сил відносно третьої точки С, що не лежить на лінії АВ не дорівнює нулю.

Це означає: для рівноваги довільно розташованих сил необхідно і достатньо, щоб алгебраїчна сума моментів усіх сил відносно кожної із трьох довільних точок площини, які не лежать на одній прямій, дорів­нювала нулю.

Треба зазначити, що в усіх випадках для системи довільно розта­шованих сил можна скласти тільки три незалежних рівняння рівноваги. Тому в задачах повинно бути не більше трьох невідомих.