Зчеплення і тертя ковзання

Перші дослідження явища тертя сягають до робіт Леонардо да Вінчі. Детальні дослідження законів тертя почав французький механік Г.Амонтон (1663…1705). У 1781 р. Ш.Кулон (1736-1806), французький фізик і механік, опублікував «Теорію простих машин з точки зору їх частин», в якій виклав теорію тертя і сформулював закони тертя.

Розглянемо тверде тіло, що знаходиться у стані спокою на горизонтальній площині (рис.11.1). У випадку, коли тіло і площина є абсолютно гладкими, то реакція в’язі (площини) напрямлена по нормалі до спільної дотичної, тобто перпендикулярно до площини (рис.11.1 а), а спроба прикласти до тіла будь-яку, навіть нескінченно малу силу, не перпендикулярну до площини, порушить стан рівноваги – тіло почне рухатись (ковзати) по площині. Зовсім інша картина спостерігається при розгляданні стану рівноваги реальних тіл, поверхні яких є більш чи менш шорсткими. Прикладемо до тіла горизонтальну силу 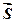, величину якої будемо поступово збільшувати від нульового значення. На певному інтервалі збільшення сили тіло буде залишатися у стані спокою, що можливо лише при появі протидіючої сили, такої, що зрівноважує силу 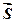. Силу, яка виникає в площині стикання тіл, називають силою зчеплення або силою тертя ковзання при стані спокою - 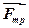(рис.11.1 б).

Поява сили зчеплення спричиняє відхилення від нормалі повної реакції площини, і її розглядають як геометричну суму нормальної і тангенціальної складових, причому остання і є силою зчеплення: 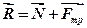. Тіло залишається у стані спокою при зміні модуля сили 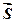від нуля до певного значення її 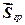, при якому починається ковзання. Відповідно і сила зчеплення (сила тертя спокою) зростає від нуля до деякого максимального значення 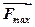, більше якого вона бути не може (рис.11.1 .в).

Тобто:

.

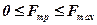(11.1)

Досвід показує, що максимальне значення сили тертя спокою пропорційне силі нормального тиску тіла на поверхню або за модулем нормальній реакції:

.

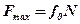(11.2)

Коефіцієнт пропорційності 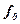називають статичним коефіцієнтом тертя. Він є безрозмірною величиною, яка залежить від матеріалу стичних поверхонь, чистоти їх обробки, температури, тощо. В той же час його можна вважати незалежним від площі контакту тіл.

Умова 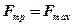є умовою граничної рівноваги тіла в стані спокою. При найменшому перевищенні сили 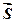своєї граничної величини 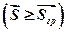тіло починає ковзати.

При ковзанні тіла по шорсткій поверхні до нього прикладена сила тертя ковзання. Напрям цієї сили протилежний напряму руху тіла, а модуль сили тертя ковзання визначають за формулою:

,

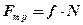(11.3)

де 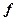- коефіцієнт тертя ковзання (динамічний коефіцієнт тертя), величина також безрозмірна і, в певній мірі, залежна від швидкості відносного руху стичних тіл.

В більшості випадків при зростанні відносної швидкості взаємодіючих сил коефіцієнт тертя ковзання 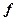спочатку незначно спадає від значення 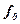, а потім зберігає майже стале значення.

В наближених технічних розрахунках нехтують деякою різницею коефіцієнтів тертя і приймають .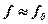

Якщо під дією прикладених сил тіло знаходиться в рівновазі, то згідно з нерівністю (11.1) в межах зони рівноваги сила тертя може приймати значення від нуля до 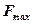. Тому при фіксованій величині нормальної реакції 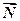повна реакція поверхні також може змінюватися від 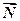до свого максимального значення 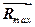, а кут відхилення 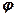реакції від нормалі буде зростати від нуля до певного граничного значення 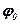(рис.11.1в).

Кут 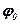, який утворює 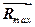з нормаллю 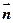називають кутом зчеплення, або кутом тертя. З рис.11.1 в видно, що 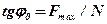, а оскільки 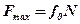, то:

.

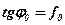(11.4)

Має місце така особливість області конуса тертя - конуса, описаного лінією дії максимальної повної реакції навколо напряму нормалі до площини стикання тіл – будь-яка за величиною сила 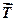, що утворює з нормаллю кут 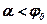(тобто розташована всередині цієї області) не може надати руху тілу, яке знаходиться в стані рівноваги на шорсткій поверхні (рис.11.2). Саме цим пояснюються відомі в техніці явища заклинювання і самогальмування тіл.

Рис.11.2

З цієї формули виходить, що утримуюча сила не залежить від діаметра циліндра. Практично важливим є та обставина, що за рахунок збільшення кута охоплення можна значно зменшити утримуючу силу. Наприклад, натяг в 1 кН можна урівноважити силою 2Н, якщо двічі ( 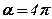) обернути конопляний канат навколо дерев’яного стовпа.

За формулою Ейлера визначають натяги ведучої ( 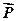) і веденої ( 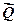) частин пасової передачі, яка часто використовується в сільгоспмашинах.

Тертя кочення

Тертям кочення називають опір, який виникає при коченні одного тіла по поверхні другого.

Нехай круглий циліндричний коток радіусом 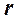і вагою 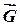знаходиться на горизонтальній шорсткій площині. Прикладемо до осі котка певну силу 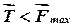. Тоді в точці стикання А котка з площиною, крім нормальної реакції 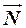повинна виникнути і сила тертя ковзання 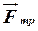( 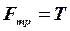), яка буде перешкоджати ковзанню котка по площині (рис.11.3).

Але при такій схемі розташування сил утворюється нічим не зрівноважена пара сил ( 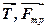), яка повинна була б викликати кочення при будь-якій малій силі 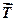, чого реально не спостерігається.

Справа у тому, що через деформації поверхонь реальних стичних тіл їх торкання відбувається по певній площадці ВАD, причому інтенсивність тиску вздовж якої збільшується від краю В до краю D. В результаті реакція 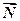площини, що є рівнодіючою цих тисків, виявляється зміщеною у бік дії сили 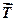(рис. 11.4). Таким чином, до котка в стані рівноваги прикладені дві взаємно зрівноважені пари сил ( 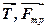) і ( 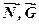). Перша з них прагне зрушити коток, друга – протидіє руху.

Рис.11.4

Доки коток знаходиться у рівновазі збільшення сили 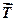, а, відповідно, і пари ( 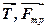), викликає зростання протидіючої пари, момент якої називають моментом опору коченню, або моментом тертя кочення. Очевидно, що зростання момента опору коченню можливе тільки за рахунок збільшення відстані .

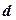В стані граничної рівноваги 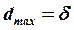і максимальний момент опору коченню:

,

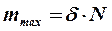(11.5)

де 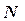- нормальна складова повної реакції площини.

Коефіцієнт пропорційності 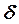, котрий має лінійну розмірність, називають коефіцієнтом тертя кочення. Його величина залежить від матеріалу тіл, фізичного стану їх поверхонь і визначається експериментально.

Якщо активні сили, що діють на коток, звести до точки контакту А з площиною (деформаціями котка і поверхні нехтуємо), то в загальному випадку дістанемо головний вектор сил 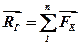і головний момент 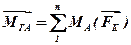. Головний вектор прагне змусити коток ковзати, а головний момент – котитися (рис.11.5).

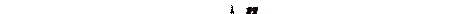
Рис. 1.25

Для того, щоб коток не котився, необхідно виконання умови:

.

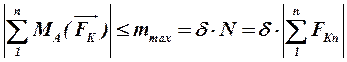(11.6)

Для того, щоб коток не ковзав, необхідно, щоб:

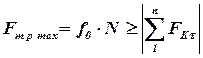
або:

.

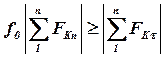(11.7)

Таким чином, відсутність ковзання і кочення буде зберігатися при одночасному виконанні умов (1.29) і (1.30).

Кочення без ковзання відповідає такому співвідношенню:

.

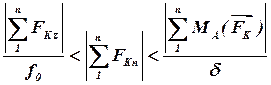(11.8)

Активні сили, які прикладені до котків у вигляді коліс (рис.11.6), крім сили ваги 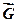звичайно складаються із сили 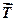, прикладеної до центра колеса, паралельно спільній дотичній в точці А, і пари сил з моментом 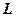, що прагне котити колесо.

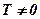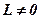Колеса, для яких і , називають ведено-ведучими; якщо 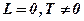, то колесо називають веденим; при 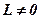і 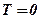колесо є ведучим.

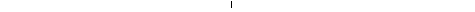
Рис.11.6

Питання для самоконтролю

1. Якими причинами можна пояснити виникнення тертя ковзання?

2. Від чого залежить величина сили тертя ковзання при спокою і в яких межах вона змінюється?

3. Що являє собою конус тертя і яку знаменну властивість має область у середині його?

4. Поясніть причини виникнення тертя кочення.

5. Від яких факторів залежить величина опору коченню і в яких межах змінюється момент сил опору коченню?

6. У чому полягає фізична різниця між коефіцієнтами тертя ковзання і кочення?

7. За якими формулами визначаються максимальна сила тертя ковзання спокою і максимальний момент сил опору коченню?

8. При яких умовах кочення відбувається без ковзання?

9. При яких умовах кочення буде відбуватися із ковзанням?

10. Коток радіуса 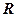котиться без ковзання по площині, що розташована під кутом 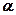до горизонту. Визначити коефіцієнт тертя кочення.

11. При відомих коефіцієнтах тертя ковзання 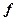і кочення 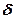котка радіуса 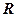визначити умови початку: а) чистого кочення і б) чистого ковзання котка на площині, що нахилена під кутом 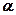до горизонту.

12. Наведіть математичний вираз умови рівноваги гнучкого тіла на негладкій циліндричній поверхні (формула Ейлера).

Заняття № 12

Практичне заняття № 2Визначення реакції опори балочних систем.

Заняття № 13

Тема: Просторова система сил.