Методичні вказівки та приклади розв'язання задач

При розв'язанні задач статики зручно дотримувати такої послідовності:

1) виділяємо тверде тіло (або сукупність тіл), реакції опор якого потрібно визначити. При дії збіжної системи сил необхідно виділяти не тіло, а точку, в якій сили збігаються;

2) схематично зображуємо вибране тіло. При цьому необхідно відкинути усі накладені на тіло в'язі і їх дію замінити реакціями в'язей;

3) при достатньому досвіді не обов'язково зображати окремо тіло,

звільнене від в'язей. Можна на загальному рисунку (при наявності в'язей) показати реакції в'язей;

4) прикласти до тіла (або точки) задане навантаження;

5) вибрати початок і напрямки осей декартових координат;

6) розв'язання задачі спрощується, якщо вісі координат спрямувати паралельно або перпендикулярно більшості сил і реакцій;

7) визначити вид одержаної системи сил і скласти відповідні рівняння рівноваги.

8) розв'язати систему рівнянь і дослідити отримані результати.

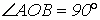Задача 1.Тягар Р вагою 100 кН підтримується за допомогою каната, перекинутого через блок О та закріпленого на барабані лебідки Е . Визначити зусилля в стержнях АО , ОВ , ОС крана, якщо площина АОВ горизонтальна, АД=ДВ , ОА=ОВ , , і (рис. 10.4).

Розв'язання

Рис. 13.4

При розв'язанні задачі будемо дотримуватися послідовності, яку викладено вище.

1) Розглянемо рівновагу шарніра О .

2) Відкинемо усі накладені на тіло в'язі, а їх дію замінимо реакціями в'язей. В'язями шарніру О є стержні АО , OC , OB . Так як стержні закріплені шарнірно і їх вагою ми нехтуємо, то реакції стержнів S_A , S_B , S_C спрямовані уздовж осей цих елементів.

3) Прикладемо до точки O всі задані навантаження. Вважаємо, що стержні розтягнуті, тобто реакції спрямовані від вузла O . Таким чином на вузол O діє система збіжних сил, яка складається з реакцій в'язей S_A , S_B , S_C та ваги тягаря 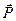. Так як натяг канату у всіх точках однаковий, то .

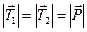4) Виберемо систему координат Lxyz так, щоб сили , , 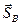, , 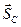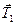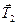розташовувались в координатних площинах; вісь Dz спрямуємо перпендикулярно до площини OAB ; початок координат виберемо в точці D , а вісі Dx та Dy спрямуємо відповідно по прямих AB та OD . Тоді сили , та 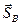будуть розташовані в площині xDy , а сили 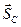, , 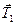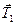- в площині zDy . При такому виборі координатних осей легко визначити кути, які утворюються векторами сил з координатними осями, і проекції сил на вісі.

5) Для просторової системи збіжних сил умови рівноваги мають вигляд:

, ,

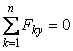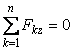
При визначенні проекцій сил, що розташовані в площині AOB , на вісі Dx і Dy , що трикутник OAB є рівнобічний, так як OA=OB . Тому пряма OD є бісектрисою кута і .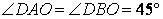

Із рис. 7.3 видно, що трикутник AOB є рівнобічний ( OA=OB ), пряма О D є бісектрисою кута , .

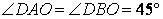Тоді проекції S_Ax , S_Ay ,S_Bx , S_By дорівнюватимуть

, ,

, .

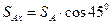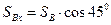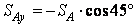Сили 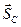, , 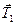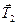розташовані в площині zDy , їх проекції на вісь Dx дорівнюють:

.

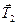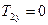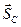Сила паралельна осі Dz , тому і . Кути між силою та осями Dz , Dy відповідно дорівнюють 60⁰ і 30⁰ , тому

, .

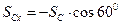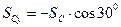Кут між силою 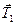і віссю Dy дорівнює , тому

.

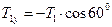Проекція сили 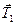на вісь Dz дорівнює

.

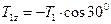Враховуючи визначені проекції сил, запишемо умови рівноваги

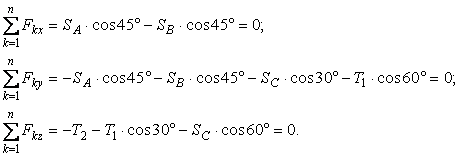
Підставляючи значення тригонометричних функцій, отримаємо:

,

,

.

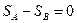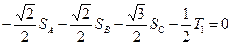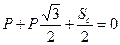Розв'язуючи цю систему трьох рівнянь, визначимо невідомі S_A ,S_B , S_C :

.

.

.

.

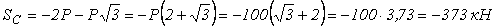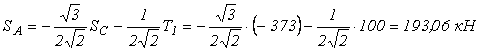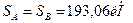Від’ємне значення сили 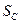показує, що стержень СО не розтягнутий, як ми прийняли, а стиснутий.

Питання для самоконтролю

1. При яких умовах тверде тіло буде знаходитись у стані рівноваги, якщо до нього прикладені три сили?

2. Чи можлива рівновага трьох збіжних сил, що не лежать в одній площині?

3. Що таке в'язь? У чому полягає суть принципу звільнення від в'язей

4. Як визначається напрям рівнодіючої системи збіжних сил при побудові силового багатокутника?

5. За якими формулами визначають модуль і напрям рівнодіючої системи збіжних сил?

6. Відомо, що сума проекцій просторової системи збіжних сил на осі Ох і Оу прямокутної координатної системи Охуz дорівнює нулю. Що можна сказати про рівнодіючу цієї системи сил?

7. Відомо, що сума проекцій плоскої системи збіжних сил на горизонтальну вісь Ох дорівнює нулю. Що можна сказати про рівнодіючу цієї системи сил?

8. У певній точці тіла прикладені три, рівні за модулем, сили, які розташовані в одній площині під кутом 120° одна до одної. Чому дорівнює рівнодіюча цих сил? Розв'язати питання геометрично і аналітично.

9. Визначити лінію дії і напрям реакції шарніра А, якщо важка однорідна балка АВ в точці С вільно спирається на гладкий виступ стіни: а) АС=СВ;

б) АС>СВ; в) АС <СВ .

10. Сформулюйте теорему Варіньона для системи збіжних сил і наведіть приклади її практичного використання при розв’язанні задач.

Заняття № 14

Тема: Просторова система сил.