Просторова система паралельних сил Три рівняння рівноваги просторової системи паралельних сил.

Користуючись загальними рівняннями просторової системи довільно розташованих сил, можна одержати залежності для зведення та рівноваги просторової системи паралельних сил.

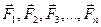Нехай дано систему паралельних сил /рис. 14.7/. Оскільки вибір координатних осей довільний, то візьмемо вісь Z паралельною даним силам. За центр зведення сил нехай буде точка О. Після зведення системи заданих сил до цього центра одержимо силу, яку прикладемо в центрі зведення і яка дорівнює головному вектору даних сил 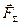, і пару сил з моментом, що дорівнює головному моменту 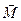всіх сил відносно центра зведення. Головний вектор і головний момент заданої системи сил визначають за тими самими залежностями /14.4/- /14.11/, що і для просторової системи довільно розташованих сил.

Рис. 14.7

При зведенні системи сил у просторі можливі такі випадки:

1/ головний вектор дорівнює нулю, а головний момент не дорівнює нулю / 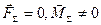/. Система сил зводиться до пари з моментом, який дорівнює сумі моментів цих сил відносно центра зведення;

2/ головний вектор не дорівнює нулю, а головний момент дорівнює нулю/ 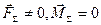/. Система сил зводиться до рівнодіючої, яка дорівнює головному вектору 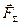і лінія дії якої проходить через центр зведення;

3/ головний вектор і головний момент дорівнюють нулю / 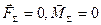/. Система сил взаємно врівноважується.

Використовуючи рівняння рівноваги для просторової системи довільно розташованих сил /14.11/ і враховуючи, що сума проекцій сил на осі, перпендикулярні силам, завжди дорівнює нулю /незалежно від того, знаходиться система сил в рівновазі чи ні/ і моменти кожної з сил відносно осі, паралельній цим силам, дорівнюють нулю, одержують рівняння рівноваги для просторової системи паралельних сил.

Таким чином, для просторової системи паралельних сил залишаються три рівняння рівноваги.

Отже, для рівноваги просторової системи паралельних сил необхідно і достатньо, щоб сума проекцій усіх сил на вісь, паралельну силам, і алгебраїчна сума моментів усіх сил відносно кожної з двох осей, які лежать у площині, що перпендикулярна до цих сил, дорівнювали нулю.

У випадку розташування сил /рис. 14.7/ рівняння рівноваги мають вигляд

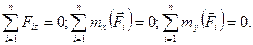
/14.12/

Необхідно зазначити, що просторова система довільно розташованих сил, для рівноваги якої необхідно шість рівнянь /14.11/, є загальним випадком розташування сил, прикладених до тіла. Наведені рівняння рівноваги для окремих випадків розташування сил можна було одержати з цих шести рівнянь, подібно тому, як це було зроблено для просторової системи паралельних сил. Для кожного випадку розташування сил можна скласти цілком визначену кількість рівнянь рівноваги, що обмежує кількість невідомих, які можна визначити. З метою узагальнення розглянутого матеріалу наводимо табл.14.1.

Таблиця 14.1

Система сил	Число незалежних рівнянь рівноваги	Рівняння рівноваги
Плоска система збіжних сил
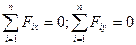
Просторова система збіжних сил
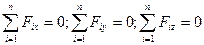
Плоска система довільно розташованих сил		1/ 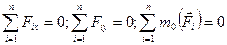,або 2/ 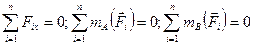,якщо вісь х не перпендикулярна до прямої АВ, або 3/ 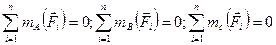,якщо точки А, В, С не лежать на одній прямій.
Плоска система паралельних сил		1/ 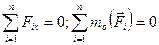, або 2/ 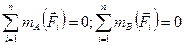.якщо точки не лежать на прямій, паралельній даним силам.
Просторова система довільно розташованих сил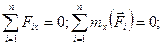
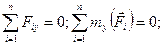
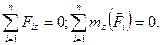
Просторова система паралельних сил

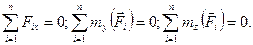
Питання для самоконтролю:

1 Сформулюйте теорему про паралельне перенесення сили. Що треба добавити при паралельному перенесенні сили, щоб не змінити її дію на тіло?

2 Чим замінюють довільну систему сил при її зведенні до заданого центра? Сформулюйте основну теорему статики (теорему Пуансо).

3 Чому дорівнює головний вектор і головний момент системи сил? Що мають спільного і чим відрізняються головний вектор системи сил та рівнодіюча?

4 В яких випадках просторова система сил зводиться до рівнодіючої?

5 В яких випадках просторова система сил зводиться до однієї пари сил?

6 Що таке динамічний гвинт (динама)? В яких випадках просторова система сил зводиться до динами?

7 Сформулюйте необхідні і достатні умови рівноваги та запишіть аналітичні рівняння рівноваги довільної просторової системи сил, просторової системи паралельних сил.

Заняття № 15

Тема: Просторова система сил.

План

1. Визначення реакцій опори просторово навантажених систем.

2. Складання рівнянь рівноваги для просторово навантажених валів.

ЛІТЕРАТУРА ОСНОВНА

ЛІТЕРАТУРА ДОДАТКОВА

Студенти повинні знати: рівняння рівноваги просторової системи довільно розташованих сил, напрямки реакцій опори просторово навантажених валів.

Студенти повинні вміти: Складати рівняння рівноваги просторової системи довільно розташованих сил та розвязувати їх .