Визначення центра системи паралельних сил
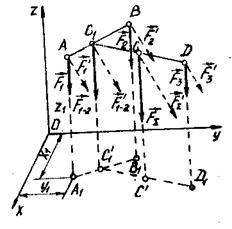 Рис. 17.3
Рис. 17.3
Узагальнимо поняття про центр паралельних сил на систему паралельних сил. Нехай дано кілька паралельних сил 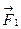
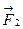 ,
, 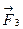 напрямлених в один бік, які утворюють деяку просторову систему сил /рис. 17.3/. Знаючи правило додавання двох паралельних сил, шляхом послідовного додавання можна знайти рівнодіючу і для будь-якої системи паралельних сил. Для цього складемо спочатку дві сили
напрямлених в один бік, які утворюють деяку просторову систему сил /рис. 17.3/. Знаючи правило додавання двох паралельних сил, шляхом послідовного додавання можна знайти рівнодіючу і для будь-якої системи паралельних сил. Для цього складемо спочатку дві сили 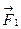 і
і 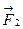 і знайдемо їх рівнодіючу
і знайдемо їх рівнодіючу 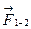 .Вона буде паралельна складовим і напрямлена в той самий бік. Модуль її
.Вона буде паралельна складовим і напрямлена в той самий бік. Модуль її 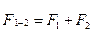 Точка
Точка 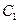 її прикладання лежить на лінії АВ і знаходиться з пропорції
її прикладання лежить на лінії АВ і знаходиться з пропорції
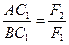 /17.6/
/17.6/
Додаючи сили 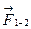 і
і 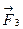 знайдемо рівнодіючу
знайдемо рівнодіючу 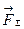 - усіх трьох сил. Вона також буде паралельна складовим і напрямлена в той самий бік. Модуль рівнодіючої дорівнює сумі модулів складових сил
- усіх трьох сил. Вона також буде паралельна складовим і напрямлена в той самий бік. Модуль рівнодіючої дорівнює сумі модулів складових сил
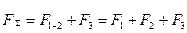 /17.7/
/17.7/
У загальному випадку залежність /17.7/ має вигляд
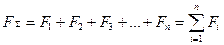 /17.8/
/17.8/
Точка С прикладання рівнодіючої визначається з пропорції
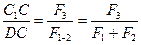
Повернувши всі сили системи навколо їх точок прикладання в один і той же бік на будь-який однаковий кут 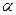 . /на рис. 17.3 / сили показано штриховими лініями/, дістанемо нову систему паралельних сил з такими самими модулями і точками прикладання складових, але з іншими лініями Дії сил. Послідовно додаючи сили нової системи, дістанемо, що рівнодіюча
. /на рис. 17.3 / сили показано штриховими лініями/, дістанемо нову систему паралельних сил з такими самими модулями і точками прикладання складових, але з іншими лініями Дії сил. Послідовно додаючи сили нової системи, дістанемо, що рівнодіюча 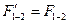 Дорівнює за модулем сумі модулів складових
Дорівнює за модулем сумі модулів складових 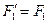 і
і 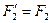 і паралельна
і паралельна 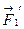 і
і 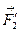 тобто її лінія дії повертатиметься в той самий бік на такий самий кут
тобто її лінія дії повертатиметься в той самий бік на такий самий кут 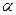 що і складових. Положення точки С прикладання рівнодіючої
що і складових. Положення точки С прикладання рівнодіючої 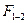 яке визначається також пропорцією /17,6/, залишається незмінним, оскільки не змінилися ні модулі сил, ні відрізок АВ прямої, що з’єднує їх точки прикладання. Міркуючи так само, знайдемо, що не зміниться положення точки прикладання рівнодіючої
яке визначається також пропорцією /17,6/, залишається незмінним, оскільки не змінилися ні модулі сил, ні відрізок АВ прямої, що з’єднує їх точки прикладання. Міркуючи так само, знайдемо, що не зміниться положення точки прикладання рівнодіючої 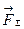 усіх сил даної системи. Отже, точка С буде центром даної системи паралельних сил.
усіх сил даної системи. Отже, точка С буде центром даної системи паралельних сил.
Щоб одержати формули для визначення координат центра системи параледьних сил, позначимо координати точок прикладання сил 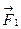 ,
, 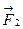 ,
, 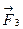 ,
, 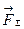 відповідно через
відповідно через 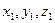 /точка А /,
/точка А /, 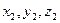 /точка В/,
/точка В/, 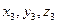 /точка D/,
/точка D/, 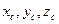 /точка СІ. Обчислимо спочатку абсцису Хс. Центра паралельних сил. Для цього запишемо рівняння моментів усіх сил відносно осі
/точка СІ. Обчислимо спочатку абсцису Хс. Центра паралельних сил. Для цього запишемо рівняння моментів усіх сил відносно осі 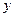 Як було показано раніше / теорема Варіньона /, момент рівнодіючої сили
Як було показано раніше / теорема Варіньона /, момент рівнодіючої сили 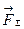 відносно координатної осі дорівнює сумі моментів усіх прикладених сил відносно цієї самої осі, тобто
відносно координатної осі дорівнює сумі моментів усіх прикладених сил відносно цієї самої осі, тобто
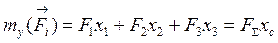 , /17.9/
, /17.9/
Звідки маємо
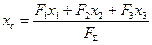 /17.10/
/17.10/
Або з урахуванням /17.7/
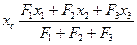 /17.11/
/17.11/
Записавши рівняння моментів усіх сил відносно осі Х за аналогією попереднім, матимемо формулу для визначення ординати:
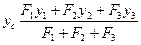 /17.12/
/17.12/
Для визначення аплікати 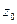 центра паралельних сил повернемо всі сили на 90°, наприклад так, щоб вони були розташовані паралельно осі у і запишемо моменти сил відносно осі х. Звідки
центра паралельних сил повернемо всі сили на 90°, наприклад так, щоб вони були розташовані паралельно осі у і запишемо моменти сил відносно осі х. Звідки
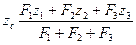 /17.13/
/17.13/
У загальному випадку, коли на тіло діє n сил, залежності /17.II/-/17.13/ набувають вигляду:
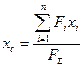
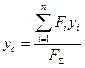
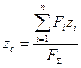 /17.14/
/17.14/
де 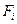 - модулі прикладених силі
- модулі прикладених силі 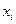
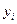
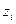 - координати точок їх прикладання
- координати точок їх прикладання
Питання для самоконтролю
1. Як визначити модуль, напрям і точку прикладання рівнодіючої двох паралельних сил?
2. Як визначити модуль і напрям рівнодіючої системи паралельних сил?
3. Що називають центром системи паралельних сил і центром ваги тіла?
4. Що називають статичним моментом площі відносно осі? В яких одиницях він вимірюється?
5. Чому дорівнює статичний момент плоскої фігури відносно осі симетрії?
6. Де знаходиться центр ваги фігур, тіл, які мають площину, вісь або центр симетрії?
7. Де знаходиться центр ваги площ прямокутника, паралелограма, трикутника, круга, об’єму кулі, конуса, піраміди?
8. Що розуміють під стійкістю рівноваги?
9. Види рівноваги. Наведіть приклади.
10. Чи мають однакові статичну й динамічну стійкість призма і піраміда, в яких основи та висоти однакові?
11. Що розуміють під кутом і коефіцієнтом стійкості?
Заняття № 18
Тема:Центр тяжіння.
План
1. Центр ваги тіла. Статичний момент інерції перерізу.
2. Положення центра ваги симетричного тіла
3. Визначення центру тяжіння простих плоских геом. фігур та стандартних профілей прокату.
4. Визначення центру тяжіння складеного перерізу.
5. Стійкість рівноваги.
ЛІТЕРАТУРА ОСНОВНА
ЛІТЕРАТУРА ДОДАТКОВА
Студенти повинні знати: Формули для визначення положення центру паралельних сил, а також Формули для визначення положення центру тяжіння тіл складених із тонких пластин, стрижнів, однорідних об’ємів.
Студенти повинні вміти: визначати положення цекнтру тяжиня складених плоских геометричних фігур .
Центр ваги тіла
У результаті взаємодії тіла з Землею на кожну елементарну частинку тіла діє сила ваги, яка завжди напрямлена до центра Землі. Враховуючи, що відстань тіла від центра Землі значно більша за розміри тіла, вважатимемо всі ці сили паралельними. Центр С цієї системи паралельних сил ваги називається центром ваги тіла.
За будь-якого положення тіла в просторі сили ваги його окремих частинок будуть прикладені в одних і тих самих точках і паралельні між собою. Може лише, змінитися положення лінії дії цих сил відносно тіла. Але рівнодіюча 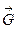 системи сил ваги
системи сил ваги 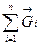 окремих частинок тіла буде завжди проходити через одну і ту саму точку С - центр паралельних сил ваги частинок тіла
окремих частинок тіла буде завжди проходити через одну і ту саму точку С - центр паралельних сил ваги частинок тіла 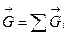
Центром ваги тіла є така, незмінно зв’язана з цим тілом геометрична точка, через яку проходить лінія дії сили ваги даного тіла за будь-якого його положення в просторі.
Положення центра ваги тіла залежить тільки від форми тіла й розподілу в ньому матеріальних частинок. Причому центр ваги може лежати й поза тілом /наприклад, центр ваги кільця, порожнистого вала, труби тощо/.
Отже, центр ваги тіла є центром паралельних сил - сил ваги окремих його частинок. Тому для визначення положення центра ваги можна скористатися формулами для координат центра паралельних сил /17.14/.
Якщо в цих формулах модулі сил 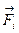 замінимо модулями сили ваги
замінимо модулями сили ваги 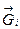 окремих частинок тіла, а рівнодіючу - силою ваги
окремих частинок тіла, а рівнодіючу - силою ваги 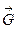 тіла, то одержимо формули координат центра ваги тіла:
тіла, то одержимо формули координат центра ваги тіла:
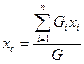
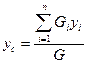
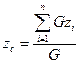 /17.15 /
/17.15 /
Формули /17.15/ використовують лише тоді, коли необхідно визначити положення центра ваги неоднорідного тіла або незмінної системи тіл з різних матеріалів. Найчастіше визначають положення центрів ваги однорідних тіл і тоді з формули /17.15/ витікає три їх різновиди.
І. Якщо тіло має вигляд плоскої або просторової решітки /дротяних гратів/, які складаються з однорідних тонких прутів, площі поперечних перерізів яких постійні, то сила ваги будь-якої прямолінійної чи криволінійної ділянки 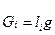 , де
, де 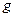 - вага одиниці довжини прутка,
- вага одиниці довжини прутка, 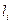 - довжина окремих ділянок решітки; загальна вага решітки
- довжина окремих ділянок решітки; загальна вага решітки 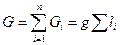
Тоді, підставивши в /7.15/ замість 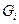 і
і 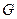 їх значення і скоротивши
їх значення і скоротивши 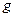 , дістанемо формули для визначення координат
, дістанемо формули для визначення координат
центра ваги тіл у вигляді решітки /каркасу/:
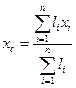
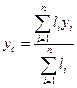
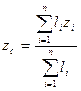 /17.16/,
/17.16/,
де 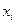
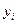
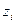 - координати центрів ваги окремих ділянок решітки довжиною
- координати центрів ваги окремих ділянок решітки довжиною 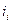 ,
,
2. Якщо тіло складено з тонких однорідних пластин /листів/ однакової товщини, то сила ваги кожної ділянки 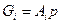 де
де 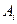 - площа окремих ділянок пластинчатої конструкції, р - вага одиниці площі пластини; сила ваги всього тіла
- площа окремих ділянок пластинчатої конструкції, р - вага одиниці площі пластини; сила ваги всього тіла 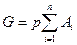 . Підшипники
. Підшипники  і
і  в /17.15/, одержимо формули координат центра ваги тіла /конструкції/, яке складено з однорідних пластин /площ/:
в /17.15/, одержимо формули координат центра ваги тіла /конструкції/, яке складено з однорідних пластин /площ/:
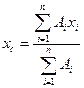
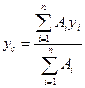
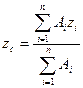 /17.17/
/17.17/
3. Подібні формули одержимо і для однорідних тіл, які складені з об’ємних частин, якщо в формулах /7.15/ замінимо 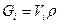 , де
, де 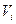 - об’єми окремих частин тіла, вага яких
- об’єми окремих частин тіла, вага яких 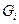 і
і 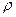 - об’ємна вага
- об’ємна вага
тіла /вага одиниці об’єму тіла/ 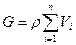
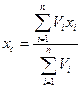
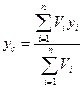
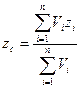 /17.18/
/17.18/
Для плоских фігур із трьох формул /17.17/ використовуються тільки перші дві /для визначення 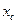 і
і 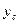 /.
/.
Дата добавления: 2016-01-26; просмотров: 1844;
