Центр ваги кругового сектора.
Нехай буде заданий круговий сектор OADB з центральним кутом 2 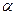 /рис. 17.10/. Поділимо сектор на елементарні сектори, які можна прийняти за рівнобедрені трикутники AOA7 , A7 0Aг і т.д., висотою, що дорівнює радіусу r сектора. Центр ваги кожного елементарного сектора /трикутника/ лежить на Його висоті на відстані (2|3)r від вершини O а всі разом вони утворюють дугу радіуса
/рис. 17.10/. Поділимо сектор на елементарні сектори, які можна прийняти за рівнобедрені трикутники AOA7 , A7 0Aг і т.д., висотою, що дорівнює радіусу r сектора. Центр ваги кожного елементарного сектора /трикутника/ лежить на Його висоті на відстані (2|3)r від вершини O а всі разом вони утворюють дугу радіуса 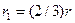 .
.
Підставивши в /7.25/ замість r значення 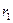 , дістанемо абсцису центра ваги кругового сектора
, дістанемо абсцису центра ваги кругового сектора
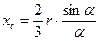 /17.25/
/17.25/
Зокрема, для півкруга 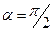
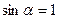 і формула /7.26/ набуде вигляду
і формула /7.26/ набуде вигляду

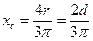 , /17.26/
, /17.26/
Де 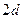 - Діаметр круга.
- Діаметр круга.
Центр ваги кругового сегмента знаходиться на радіусі 0D перпендикулярному до хорди AB /рис. 17.10/ і розташованому від центра сегмента на відстані
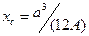 /17.27/
/17.27/
де 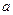 - довжина хорди AB, A - площа сегмента, яка знаходиться як різниця між площею відповідного сектора OADBтрикутника OAB, утвореного його
- довжина хорди AB, A - площа сегмента, яка знаходиться як різниця між площею відповідного сектора OADBтрикутника OAB, утвореного його
Рис. 17.10
радіусами OB, OA і хордою AB, тобто
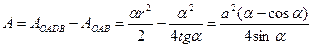 /17.28/
/17.28/
Тут 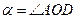 - кут; рад;
- кут; рад; 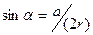

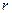 - радіус сегмента;
- радіус сегмента; 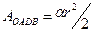 - площа сектора
- площа сектора 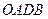 ;
; 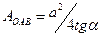 - площа трикутника ОАВ.
- площа трикутника ОАВ.
центрів ваги фігур складної форми.
Рис. 17.11
Метод групування.
Для визначення положення центра ваги фігури складної довільної форми /рис. 7.12,а/ її розбивають на прості: прямокутник, трикутник і півкруг, центри ваги яких відомі /точки 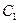 ,
, 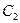 ,
, 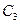 . Координати центрів ваги відповідно
. Координати центрів ваги відповідно 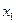 ,
, 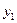 ;
; 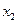 ,
, 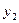 ;
; 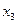 ,
, 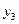 За формулою /7.17/ або /7.18/ визначають координати центра ваги всієї фігури:
За формулою /7.17/ або /7.18/ визначають координати центра ваги всієї фігури:
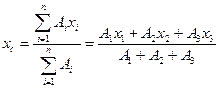

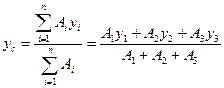

Рис. 17.12 а/ б/
Метод від’ємних мас. Для визначення положення центра ваги фігури, в якої вирізаний круг /рис. 17.12, б/, її розбивають на півкруг, трикутник, круг. Позначають площі і координати центрів ваги простих фігур: 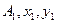 ;
; 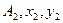 ;
; 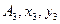 . Круг вважають від’ємною площиною /у тіла - від’ємна маса/, тому що він вирізається. Тоді, координати центра ваги всієї фігури визначаються так:
. Круг вважають від’ємною площиною /у тіла - від’ємна маса/, тому що він вирізається. Тоді, координати центра ваги всієї фігури визначаються так:
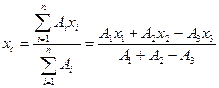
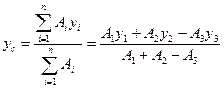
Так само визначають положення центра ваги тіл складної форми. Для цього їх розбивають на простіші тіла, вага /об’єм/ і положення центра ваги яких відомі або легко знайти. Розрахунки ведуться відповідно за формулами /17.І5/-/17.І8/. У табл. 7.1 наведені формули для визначення положення центрів ваги деяких простих геометричних ліній, фігур і тіл, якими можна скористатися для таких розрахунків
Таблиця 17.1
Положення центра ваги деяких простих геометричних ліній, фігур і тіл
| Рисунок | Положення центра ваги | |

| Дуга кола 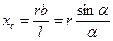 , де , де 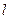 - довжина дуги; - довжина дуги; 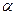 - кут.для - кут.для 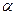 = = 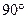
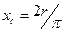 ; ; 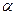 = = 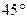 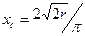 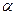 = = 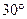 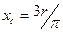
| |

| Площа трикутника. Центр ваги знаходиться на перетині медіан. Його положення також можна знайти через координати 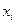 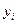 вершин трикутника за формулами / і=1,2,3/ вершин трикутника за формулами / і=1,2,3/
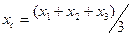
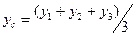
| |

| Площа трапеції 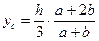 . Для знаходження графічним способом центра ваги С трапецію поділяють на два трикутники, центри ваги яких . Для знаходження графічним способом центра ваги С трапецію поділяють на два трикутники, центри ваги яких 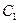 , , 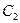 центр ваги С знаходиться на перетині медіани КІ. і лінії центр ваги С знаходиться на перетині медіани КІ. і лінії 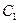 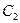
| |
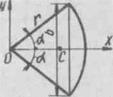
| Площа кругового сектора 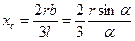 , де , де 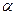 - кут, рад.
При - кут, рад.
При 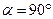 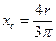
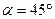 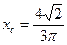
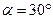 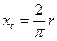
| |
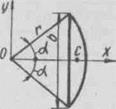
| Площа кругового сегмента 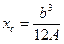 , де , де 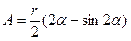 площа сегмента. площа сегмента. 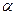 - кут, рад. - кут, рад.
| |
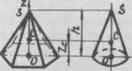
| Бічна поверхня піраміди і конуса 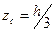 -Центр ваги лежить на прямій -Центр ваги лежить на прямій 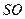 де О - центр ваги периметра основи
Об’єм піраміди і конуса де О - центр ваги периметра основи
Об’єм піраміди і конуса 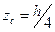 Центр ваги лежить на прямій Центр ваги лежить на прямій 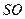 ,де О - центр ваги площі основи ,де О - центр ваги площі основи
| |
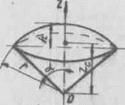
| Об’єм кульового сектора
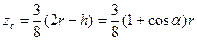 . Для об’єму півкулі . Для об’єму півкулі 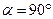
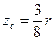
| |
| Об’єм кульового сегмента
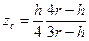
|
Дата добавления: 2016-01-26; просмотров: 2802;
